
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;
(3)登山多长时间时,甲、乙两人距地面的高度差为70米?

【答案】(1)10;30;(2)y=![]() ;(3)3分钟、10分钟或13分钟.
;(3)3分钟、10分钟或13分钟.
【解析】
(1)根据速度=高度÷时间即可算出甲登山上升的速度;根据高度=速度×时间即可算出乙在A地时距地面的高度b的值;
(2)分0≤x≤2和x≥2两种情况,根据高度=初始高度+速度×时间即可得出y关于x的函数关系;
(3)找出甲登山全程中y关于x的函数关系式,令二者做差等于50即可得出关于x的一元一次方程,解之即可得出结论.
解:(1)(300-100)÷20=10(米/分钟),
b=15÷1×2=30.
故答案为:10;30.
(2)当0≤x≤2时,y=15x;
当x≥2时,y=30+10×3(x-2)=30x-30.
当y=30x-30=300时,x=11.
∴乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式为y=![]() .
.
(3)甲登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式为y=10x+100(0≤x≤20).
当10x+100-15x=70时,解得:x=6(舍去);
当10x+100-(30x-30)=70时,解得:x=3;
当30x-30-(10x+100)=70时,解得:x=10;
当300-(10x+100)=70时,解得:x=13.
答:登山3分钟、10分钟或13分钟时,甲、乙两人距地面的高度差为70米.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,﹣4),B(3,﹣2),C(6,﹣3).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)以M点为位似中心,在网格中画出△A1B1C1的位似图形△A2B2C2 , 使△A2B2C2与△A1B1C1的相似比为2:1;
(3)若每一个方格的面积为1,则△A2B2C2的面积为 . 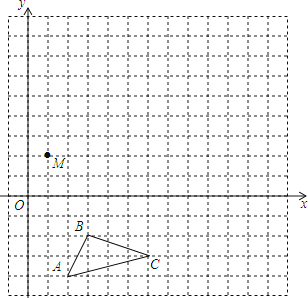
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表反映的是某地区电的使用量x(千瓦时)与应交电费y(元)之间的关系,下列说法不正确的是( )
用电量x(千瓦时) | 1 | 2 | 3 | 4 | … |
应交电费y(元) | 0.55 | 1.1 | 1.65 | 2.2 | … |
A. x与y都是变量,且x是自变量,y是x的函数
B. 用电量每增加1千瓦时,电费增加0.55元
C. 当交电费20.5元时,用电量为37千瓦时
D. 若用电量为8千瓦时,则应交电费4.4元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果店王阿姨到水果批发市场打算购进一种水果销售,经过还价,实际价格每千克比原来少2元,发现原来买这种水果80千克的钱,现在可买88千克. 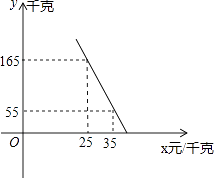
(1)现在实际购进这种水果每千克多少元?
(2)王阿姨准备购进这种水果销售,若这种水果的销售量y(千克)与销售单价x(元/千克)满足如图所示的一次函数关系. ①求y与x之间的函数关系式;
②请你帮王阿姨拿个主意,将这种水果的销售单价定为多少时,能获得最大利润?最大利润是多少?(利润=销售收入﹣进货金额)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读材料)
∵![]() <
<![]() <
<![]() ,即2<
,即2<![]() <3,
<3,
∴1<![]() <2.
<2.
∴![]() ﹣1的整数部分为1.
﹣1的整数部分为1.
∴![]() ﹣1的小数部分为
﹣1的小数部分为![]() ﹣2
﹣2
(解决问题)9的小数部分是 ;
我们还可以用以下方法求一个无理数的近似值.
阅读理解:求![]() 的近似值.
的近似值.
解:设![]() =10+x,其中0<x<1,则107=(10+x)2,即107=100+20x+x2.
=10+x,其中0<x<1,则107=(10+x)2,即107=100+20x+x2.
因为0<x<1,所以0<x2<1,所以107≈100+20x,解之得x≈0.35,即![]() 的近似值为10.35.
的近似值为10.35.
理解应用:利用上面的方法求![]() 的近似值(结果精确到0.01).
的近似值(结果精确到0.01).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰△ABC中,∠ACB=90°,且AC=1.过点C作直线l∥AB,P为直线l上一点,且AP=AB.则点P到BC所在直线的距离是( )
A.1
B.1或 ![]()
C.1或 ![]()
D.![]() 或
或 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】妈妈买回6个粽子,其中1个花生馅,2个肉馅,3个枣馅.从外表看,6个粽子完全一样,女儿有事先吃.
(1)若女儿只吃一个粽子,则她吃到肉馅的概率是;
(2)若女儿只吃两个粽子,求她吃到的两个都是肉馅的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,菱形ABCD中,∠A=60°,点P从A出发,以2cm/s的速度沿边AB、BC、CD匀速运动到D终止,点Q从A与P同时出发,沿边AD匀速运动到D终止,设点P运动的时间为t(s).△APQ的面积S(cm2)与t(s)之间函数关系的图象由图2中的曲线段OE与线段EF、FG给出.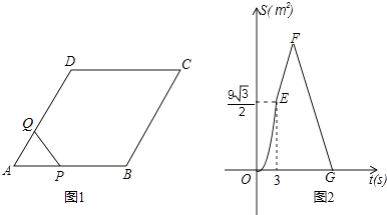
(1)求点Q运动的速度;
(2)求图2中线段FG的函数关系式;
(3)问:是否存在这样的t,使PQ将菱形ABCD的面积恰好分成1:5的两部分?若存在,求出这样的t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为使高一新生入校后及时穿上合身的校服,现提前对某校九年级三班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6个型号):
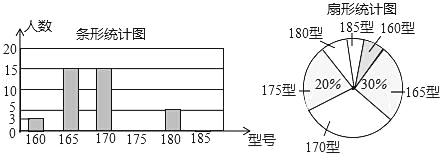
根据以上信息,解答下列问题:
(1)该班共有 名学生;
(2)补全条形统计图;
(3)该班学生所穿校服型号的众数为 ,中位数为 ;
(4)如果该校预计招收新生1500名,根据样本数据,估计新生穿170型校服的学生大约有多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com