
【题目】(阅读材料)
∵![]() <
<![]() <
<![]() ,即2<
,即2<![]() <3,
<3,
∴1<![]() <2.
<2.
∴![]() ﹣1的整数部分为1.
﹣1的整数部分为1.
∴![]() ﹣1的小数部分为
﹣1的小数部分为![]() ﹣2
﹣2
(解决问题)9的小数部分是 ;
我们还可以用以下方法求一个无理数的近似值.
阅读理解:求![]() 的近似值.
的近似值.
解:设![]() =10+x,其中0<x<1,则107=(10+x)2,即107=100+20x+x2.
=10+x,其中0<x<1,则107=(10+x)2,即107=100+20x+x2.
因为0<x<1,所以0<x2<1,所以107≈100+20x,解之得x≈0.35,即![]() 的近似值为10.35.
的近似值为10.35.
理解应用:利用上面的方法求![]() 的近似值(结果精确到0.01).
的近似值(结果精确到0.01).
科目:初中数学 来源: 题型:
【题目】如图的矩形ABCD中,E点在CD上,且AE<AC.若P、Q两点分别在AD、AE上,AP:PD=4:1,AQ:QE=4:1,直线PQ交AC于R点,且Q、R两点到CD的距离分别为q、r,则下列关系何者正确?( ) 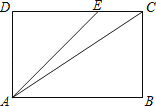
A.q<r,QE=RC
B.q<r,QE<RC
C.q=r,QE=RC
D.q=r,QE<RC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方程x2+3x﹣1=0的根可视为函数y=x+3的图象与函数 ![]() 的图象交点的横坐标,则方程x3+2x﹣1=0的实根x0所在的范围是( )
的图象交点的横坐标,则方程x3+2x﹣1=0的实根x0所在的范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在以点O为原点的平面直角坐标系中,一次函数y=﹣ ![]() x+1的图象与x轴交于点A,与y轴交于点B,点C在直线AB上,且OC=
x+1的图象与x轴交于点A,与y轴交于点B,点C在直线AB上,且OC= ![]() AB,反比例函数y=
AB,反比例函数y= ![]() 的图象经过点C,则所有可能的k值为 .
的图象经过点C,则所有可能的k值为 . 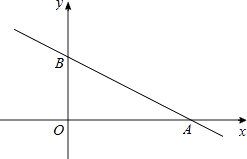
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料
如图①,△ABC与△DEF都是等腰直角三角形,∠ACB=∠EDF=90°,且点D在AB边上,AB、EF的中点均为O,连结BF、CD、CO,显然点C、F、O在同一条直线上,可以证明△BOF≌△COD,则BF=CD.
解决问题
(1)将图①中的Rt△DEF绕点O旋转得到图②,猜想此时线段BF与CD的数量关系,并证明你的结论;
(2)如图③,若△ABC与△DEF都是等边三角形,AB、EF的中点均为O,上述(1)中的结论仍然成立吗?如果成立,请说明理由;如不成立,请求出BF与CD之间的数量关系;
(3)如图④,若△ABC与△DEF都是等腰三角形,AB、EF的中点均为0,且顶角∠ACB=∠EDF=α,请直接写出 ![]() 的值(用含α的式子表示出来)
的值(用含α的式子表示出来)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;
(3)登山多长时间时,甲、乙两人距地面的高度差为70米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,且AB=8,点C为半圆上的一点.将此半圆沿BC所在的直线折叠,若圆弧BC恰好过圆心O,则图中阴影部分的面积是 . (结果保留π) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明与甲、乙两人一起玩“手心手背”的游戏.他们约定:如果三人中仅有一人出“手心”或“手背”,则这个人获胜;如果三人都出“手心”或“手背”,则不分胜负,那么在一个回合中,如果小明出“手心”,则他获胜的概率是多少?(请用“画树状图”或“列表”等方法写出分析过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com