
【题目】如图,在以点O为原点的平面直角坐标系中,一次函数y=﹣ ![]() x+1的图象与x轴交于点A,与y轴交于点B,点C在直线AB上,且OC=
x+1的图象与x轴交于点A,与y轴交于点B,点C在直线AB上,且OC= ![]() AB,反比例函数y=
AB,反比例函数y= ![]() 的图象经过点C,则所有可能的k值为 .
的图象经过点C,则所有可能的k值为 . 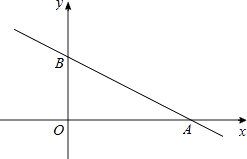
【答案】![]() 或﹣
或﹣ ![]()
【解析】解:在y=﹣ ![]() x+1中,令y=0,则x=2;令x=0,得y=1, ∴A(2,0),B(0,1).
x+1中,令y=0,则x=2;令x=0,得y=1, ∴A(2,0),B(0,1).
在Rt△AOB中,由勾股定理得:AB= ![]() .
.
设∠BAO=θ,则sinθ= ![]() ,cosθ=
,cosθ= ![]() .
.
当点C为线段AB中点时,有OC= ![]() AB,
AB,
∵A(2,0),B(0,1),
∴C(1, ![]() ).
).
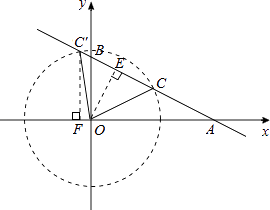
以点O为圆心,OC长为半径作圆,与直线AB的另外一个交点是C′,则点C、点C′均符合条件.
如图,过点O作OE⊥AB于点E,则AE=OAcosθ=2× ![]() =
= ![]() ,
,
∴EC=AE﹣AC= ![]() ﹣
﹣ ![]() =
= ![]() .
.
∵OC=OC′,∴EC′=EC= ![]() ,∴AC′=AE+EC′=
,∴AC′=AE+EC′= ![]() +
+ ![]() =
= ![]() .
.
过点C′作CF⊥x轴于点F,则C′F=AC′sinθ= ![]() ×
× ![]() =
= ![]() ,
,
AF=AC′cosθ= ![]() ×
× ![]() =
= ![]() ,
,
∴OF=AF﹣OA= ![]() ﹣2=
﹣2= ![]() .
.
∴C′(﹣ ![]() ,
, ![]() ).
).
∵反比例函数y= ![]() 的图象经过点C或C′,1×
的图象经过点C或C′,1× ![]() =
= ![]() ,﹣
,﹣ ![]() ×
× ![]() =﹣
=﹣ ![]() ,
,
∴k= ![]() 或﹣
或﹣ ![]() .
.
解法二:设C(m,﹣ ![]() m+1),
m+1),
根据勾股定理,m2+(﹣ ![]() m+1)2=(
m+1)2=( ![]()
![]() )2 ,
)2 ,
解得:m=﹣ ![]() 或1.
或1.
∴k= ![]() 或﹣
或﹣ ![]() .
.
所以答案是: ![]() 或﹣
或﹣ ![]() .
.


科目:初中数学 来源: 题型:
【题目】某市对一大型超市销售的甲、乙、丙3种大米进行质量检测.共抽查大米200袋,质量评定分为A、B两个等级(A级优于B级),相应数据的统计图如下: 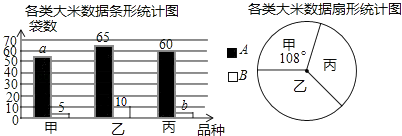
根据所给信息,解决下列问题:
(1)a= , b=;
(2)已知该超市现有乙种大米750袋,根据检测结果,请你估计该超市乙种大米中有多少袋B级大米?
(3)对于该超市的甲种和丙种大米,你会选择购买哪一种?运用统计知识简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表反映的是某地区电的使用量x(千瓦时)与应交电费y(元)之间的关系,下列说法不正确的是( )
用电量x(千瓦时) | 1 | 2 | 3 | 4 | … |
应交电费y(元) | 0.55 | 1.1 | 1.65 | 2.2 | … |
A. x与y都是变量,且x是自变量,y是x的函数
B. 用电量每增加1千瓦时,电费增加0.55元
C. 当交电费20.5元时,用电量为37千瓦时
D. 若用电量为8千瓦时,则应交电费4.4元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在梯形ABCD中,AB∥CD,∠B=90°,AB=2,CD=1,BC=m,P为线段BC上的一动点,且和B、C不重合,连接PA,过P作PE⊥PA交CD所在直线于E.设BP=x,CE=y.
(1)求y与x的函数关系式;
(2)若点P在线段BC上运动时,点E总在线段CD上,求m的取值范围;
(3)如图2,若m=4,将△PEC沿PE翻折至△PEG位置,∠BAG=90°,求BP长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果店王阿姨到水果批发市场打算购进一种水果销售,经过还价,实际价格每千克比原来少2元,发现原来买这种水果80千克的钱,现在可买88千克. 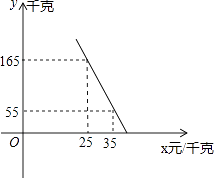
(1)现在实际购进这种水果每千克多少元?
(2)王阿姨准备购进这种水果销售,若这种水果的销售量y(千克)与销售单价x(元/千克)满足如图所示的一次函数关系. ①求y与x之间的函数关系式;
②请你帮王阿姨拿个主意,将这种水果的销售单价定为多少时,能获得最大利润?最大利润是多少?(利润=销售收入﹣进货金额)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读材料)
∵![]() <
<![]() <
<![]() ,即2<
,即2<![]() <3,
<3,
∴1<![]() <2.
<2.
∴![]() ﹣1的整数部分为1.
﹣1的整数部分为1.
∴![]() ﹣1的小数部分为
﹣1的小数部分为![]() ﹣2
﹣2
(解决问题)9的小数部分是 ;
我们还可以用以下方法求一个无理数的近似值.
阅读理解:求![]() 的近似值.
的近似值.
解:设![]() =10+x,其中0<x<1,则107=(10+x)2,即107=100+20x+x2.
=10+x,其中0<x<1,则107=(10+x)2,即107=100+20x+x2.
因为0<x<1,所以0<x2<1,所以107≈100+20x,解之得x≈0.35,即![]() 的近似值为10.35.
的近似值为10.35.
理解应用:利用上面的方法求![]() 的近似值(结果精确到0.01).
的近似值(结果精确到0.01).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】妈妈买回6个粽子,其中1个花生馅,2个肉馅,3个枣馅.从外表看,6个粽子完全一样,女儿有事先吃.
(1)若女儿只吃一个粽子,则她吃到肉馅的概率是;
(2)若女儿只吃两个粽子,求她吃到的两个都是肉馅的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要测量旗杆高CD , 在B处立标杆AB=2.5cm,人在F处.眼睛E、标杆顶A、旗杆顶C在一条直线上.已知BD=3.6m,FB=2.2m,EF=1.5m.求旗杆的高度.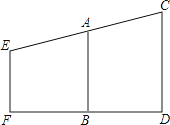
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com