
分析 利用等式的性质,和二次根式的化简方法逐步化简求得方程的解即可.
解答 解:x=$\sqrt{x-\frac{1}{x}}$+$\sqrt{1-\frac{1}{x}}$,
$\sqrt{x-\frac{1}{x}}$=x-$\sqrt{1-\frac{1}{x}}$,
两边平方得x-$\frac{1}{x}$=x2+1-$\frac{1}{x}$-2x$\sqrt{1-\frac{1}{x}}$,
x2-x-2x$\sqrt{1-\frac{1}{x}}$+1=0,
x2-x-2$\sqrt{{x}^{2}-x}$+1=0
即x2-x-1=0,
解得x=$\frac{1±\sqrt{5}}{2}$,
∵x>0,
∴x=$\frac{1+\sqrt{5}}{2}$.
故答案为:$\frac{1+\sqrt{5}}{2}$.
点评 此题考查二次根式的化简求值,解无理方程,掌握二次根式的性质和等式的性质是解决问题的关键.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,∠ACB=90°,AC=BC,点D、E分别在AB、BC上,且CD=DE,作EF⊥AB于点F.若AD=4,BF=2,求△CDE的面积.
如图,△ABC中,∠ACB=90°,AC=BC,点D、E分别在AB、BC上,且CD=DE,作EF⊥AB于点F.若AD=4,BF=2,求△CDE的面积.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0$<a<\frac{9}{16}$,且a<0 | B. | a≠0 | C. | a$>\frac{9}{16}$ | D. | a$<\frac{3}{4}$且a≠0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
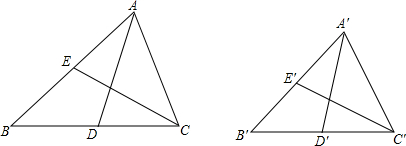
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
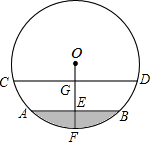 一根圆管的横截面积如图所示,圆管内原有积水的水面宽AB=40cm,水深EF=10cm,当水面上升10cm(即EG=10cm)时,水面的宽CD是多少(结果保留小数点后一位)
一根圆管的横截面积如图所示,圆管内原有积水的水面宽AB=40cm,水深EF=10cm,当水面上升10cm(即EG=10cm)时,水面的宽CD是多少(结果保留小数点后一位)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
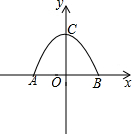 某小区的大门是如图所示的一个抛物线形状的门窗,门洞的高为4m,门洞地面的宽为6米,建立如图所示的平面直角坐标系,使抛物线的对称轴为y轴.
某小区的大门是如图所示的一个抛物线形状的门窗,门洞的高为4m,门洞地面的宽为6米,建立如图所示的平面直角坐标系,使抛物线的对称轴为y轴.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com