
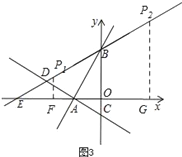
【题目】如图所示,在平面直角坐标系中,过点A(﹣![]() ,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根
,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根
(1)求线段BC的长度;
(2)试问:直线AC与直线AB是否垂直?请说明理由;
(3)若点D在直线AC上,且DB=DC,求点D的坐标;
(4)在(3)的条件下,直线BD上是否存在点P,使以A、B、P三点为顶点的三角形是等腰三角形?若存在,请直接写出P点的坐标;若不存在,请说明理由.

【答案】(1)4;(2)AC⊥AB;(3)(﹣2![]() ,1);(4)点P的坐标为(﹣3
,1);(4)点P的坐标为(﹣3![]() ,0),(﹣
,0),(﹣![]() ,2),(﹣3,3﹣
,2),(﹣3,3﹣![]() ),(3,3+
),(3,3+![]() ).
).
【解析】试题分析:
(1)解出方程后,即可求出B、C两点的坐标,即可求出BC的长度;
(2)由A、B、C三点坐标可知OA2=OCOB,所以可证明△AOC∽△BOA,利用对应角相等即可求出∠CAB=90°;
(3)容易求得直线AC的解析式,由DB=DC可知,点D在BC的垂直平分线上,所以D的纵坐标为1,将其代入直线AC的解析式即可求出D的坐标;
(4)A、B、P三点为顶点的三角形是等腰三角形,可分为以下三种情况:①AB=AP;②AB=BP;③AP=BP;然后分别求出P的坐标即可.
试题解析:
(1)∵x2﹣2x﹣3=0,
∴x=3或x=﹣1,
∴B(0,3),C(0,﹣1),
∴BC=4,
(2)∵A(﹣![]() ,0),B(0,3),C(0,﹣1),
,0),B(0,3),C(0,﹣1),
∴OA=![]() ,OB=3,OC=1,
,OB=3,OC=1,
∴OA2=OBOC,
∵∠AOC=∠BOA=90°,
∴△AOC∽△BOA,
∴∠CAO=∠ABO,
∴∠CAO+∠BAO=∠ABO+∠BAO=90°,
∴∠BAC=90°,
∴AC⊥AB;
(3)设直线AC的解析式为y=kx+b,
把A(﹣![]() ,0)和C(0,﹣1)代入y=kx+b,
,0)和C(0,﹣1)代入y=kx+b,
∴![]() ,
,
解得: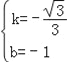 ,
,
∴直线AC的解析式为:y=﹣![]() x﹣1,
x﹣1,
∵DB=DC,
∴点D在线段BC的垂直平分线上,
∴D的纵坐标为1,
∴把y=1代入y=﹣![]() x﹣1,
x﹣1,
∴x=﹣2![]() , ∴D的坐标为(﹣2
, ∴D的坐标为(﹣2![]() ,1),
,1),
(4)设直线BD的解析式为:y=mx+n,直线BD与x轴交于点E,
把B(0,3)和D(﹣2![]() ,1)代入y=mx+n,
,1)代入y=mx+n,
∴![]() , 解得
, 解得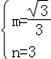 ,
,
∴直线BD的解析式为:y=![]() x+3,
x+3,
令y=0代入y=![]() x+3,
x+3,
∴x=﹣3![]() , ∴E(﹣3
, ∴E(﹣3![]() ,0),
,0),
∴OE=3![]() ,
,
∴tan∠BEC=![]() =
=![]() , ∴∠BEO=30°,
, ∴∠BEO=30°,
同理可求得:∠ABO=30°,
∴∠ABE=30°,
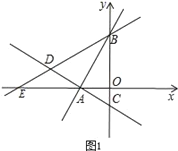
当PA=AB时,如图1,
此时,∠BEA=∠ABE=30°,
∴EA=AB,
∴P与E重合,
∴P的坐标为(﹣3![]() ,0),
,0),
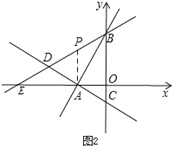
当PA=PB时,如图2,
此时,∠PAB=∠PBA=30°,
∵∠ABE=∠ABO=30°,
∴∠PAB=∠ABO,
∴PA∥BC,
∴∠PAO=90°,
∴点P的横坐标为﹣![]() ,
,
令x=﹣![]() 代入y=
代入y=![]() x+3,
x+3,
∴y=2, ∴P(﹣![]() ,2),
,2),
当PB=AB时,如图3,
∴由勾股定理可求得:AB=2![]() ,EB=6,
,EB=6,
若点P在y轴左侧时,记此时点P为P1,
过点P1作P1F⊥x轴于点F,
∴P1B=AB=2![]() ,
,
∴EP1=6﹣2![]() ,
,
∴sin∠BEO=![]() ,
,
∴FP1=3﹣![]() ,
,
令y=3﹣![]() 代入y=
代入y=![]() x+3,
x+3,
∴x=﹣3, ∴P1(﹣3,3﹣![]() ),
),
若点P在y轴的右侧时,记此时点P为P2,
过点P2作P2G⊥x轴于点G,
∴P2B=AB=2![]() ,
,
∴EP2=6+2![]() ,
,
∴sin∠BEO=![]() ,
,
∴GP2=3+![]() ,
,
令y=3+![]() 代入y=
代入y=![]() x+3,
x+3,
∴x=3, ∴P2(3,3+![]() ),
),
综上所述,当A、B、P三点为顶点的三角形是等腰三角形时,点P的坐标为(﹣3![]() ,0),(﹣
,0),(﹣![]() ,2),(﹣3,3﹣
,2),(﹣3,3﹣![]() ),(3,3+
),(3,3+![]() ).
).


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】下列说法中,正确的有( ).
①相等的圆心角所对的弧相等;
②平分弦的直径也平分弦所对的弧;
③长度相等的两条弧是等弧;
④经过圆心的每一条直线将圆分成两条等弧.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市在临桂新区正在建设的广西桂林图书馆、桂林博物馆、桂林大剧院及文化广场,建成后总面积达163500平方米,将成为我市“文化立市”和文化产业大发展的新标志,把163500平方米用科学记数法可表示为平方米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车间每天能生产甲种零件120个或乙种零件100个,甲、乙两种零件分别取2个和1个才能配套,要在80天生产最多的成套产品,甲种零件应该生产________天.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列式子从左到右变形是因式分解的是( )
A.12xy2=3xy4yB.(x+1)(x﹣3)=x2﹣2x﹣3
C.x2﹣4x+1=x(x﹣4)+1D.x3﹣x=x(x+1)(x﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠ADB=90°,点E为AB边的中点,点F为CD边的中点. 
(1)求证:四边形DEBF是菱形;
(2)若∠A=45°,求证:四边形DEBF是正方形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com