
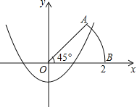
【题目】如图,以扇形![]() 的顶点
的顶点![]() 为原点,半径
为原点,半径![]() 所在的直线为
所在的直线为![]() 轴,建立平面直角坐标系,点
轴,建立平面直角坐标系,点![]() 的坐标为
的坐标为![]() ,
,![]() .现从
.现从![]() 中随机选取一个数记为
中随机选取一个数记为![]() ,则
,则![]() 的值既使得抛物线
的值既使得抛物线![]() 与扇形
与扇形![]() 的边界有公共点,又使得关于
的边界有公共点,又使得关于![]() 的方程
的方程![]() 的解是正数的概率是________.
的解是正数的概率是________.
【答案】![]()
【解析】
根据题意可以求得点A的坐标,由关于x的方程![]() 的解是正数可以求得a的取值范围,抛物线y=
的解是正数可以求得a的取值范围,抛物线y=![]() 与扇形AOB的边界有公共点,可以求得相应的a的取值范围,从而可以得到满足a的值既使得抛物线y=
与扇形AOB的边界有公共点,可以求得相应的a的取值范围,从而可以得到满足a的值既使得抛物线y=![]() 与扇形AOB的边界有公共点,又使得关于x的方程
与扇形AOB的边界有公共点,又使得关于x的方程![]() 的解是正数的a的取值范围,从而可以得到符合要求的a的值,进而求得概率是多少.
的解是正数的a的取值范围,从而可以得到符合要求的a的值,进而求得概率是多少.
由已知可得,OB=2,OA=2,∠AOB=45°,则点A的横坐标:OAcos45°=2×![]() =
=![]() ,纵坐标为:OAsin45°=2×
,纵坐标为:OAsin45°=2×![]() =
=![]() ,即点A的坐标为:(
,即点A的坐标为:(![]() ,
,![]() ),∵
),∵![]() ,解得:x=
,解得:x=![]() ,∴方程
,∴方程![]() 的解是正解时,
的解是正解时,![]() >0,得a>-1,又∵抛物线y=
>0,得a>-1,又∵抛物线y=![]() 与扇形AOB的边界有公共点,∴
与扇形AOB的边界有公共点,∴![]() 解得-2≤a≤
解得-2≤a≤![]() -1,∴a的值既使得抛物线
-1,∴a的值既使得抛物线![]() 与扇形
与扇形![]() 的边界有公共点,又使得关于
的边界有公共点,又使得关于![]() 的方程
的方程![]() 的解是正数时满足的条件是:-1<a<
的解是正数时满足的条件是:-1<a<![]() -1,∴从-2,-
-1,∴从-2,-![]() ,-1,-
,-1,-![]() ,0,
,0,![]() 中随机选取一个数记为a,则a的值既使得抛物线
中随机选取一个数记为a,则a的值既使得抛物线![]() 与扇形
与扇形![]() 的边界有公共点,又使得关于
的边界有公共点,又使得关于![]() 的方程
的方程![]() 的解是正数的概率是:
的解是正数的概率是:![]() ,故答案为
,故答案为![]() .
.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,点E、F是BC、CD的中点,且AE⊥BC,AF⊥CD.

(1)求证:AB=AD.
(2)请你探究∠EAF,∠BAE,∠DAF之间有什么数量关系?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系图象如图所示,根据图中提供的信息,有下列说法:

(1)他们都行驶了18千米;
(2)甲在途中停留了0.5小时;
(3)乙比甲晚出发了0.5小时;
(4)相遇后,甲的速度小于乙的速度;
(5)甲、乙两人同时到达目的地
其中符合图象描述的说法有( )
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系 xOy 中,直线 y ![]() x 4与 x 轴、y 轴分别交于点 A、点 B,点 D 在 y 轴的负半轴上,若将△DAB 沿着直线 AD 折叠,点 B 恰好落在 x 轴正半轴上的点 C处.
x 4与 x 轴、y 轴分别交于点 A、点 B,点 D 在 y 轴的负半轴上,若将△DAB 沿着直线 AD 折叠,点 B 恰好落在 x 轴正半轴上的点 C处.

(1)求直线 CD 的表达式;
(2)在直线 AB 上是否存在一点 P,使得 SPCD![]() SOCD?若存在,直接写出点 P 的坐标;若不存在,请说明理由.
SOCD?若存在,直接写出点 P 的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有![]() 个相同小球,分别标有不等的自然数
个相同小球,分别标有不等的自然数![]() 、
、![]() 、
、![]() 、
、![]() ,小丽每次从袋中同时摸出
,小丽每次从袋中同时摸出![]() 个小球,并计算摸出的这
个小球,并计算摸出的这![]() 个小球上数字之和,记录后将小球放回袋中搅匀,进行重复实验.实验数据如下表:
个小球上数字之和,记录后将小球放回袋中搅匀,进行重复实验.实验数据如下表:
摸球总次数 |
|
|
|
|
|
|
|
|
|
|
“和为 |
|
|
|
|
|
|
|
|
|
|
“和为 |
|
|
|
|
|
|
|
|
|
|
![]() 如果实验继续进行下去,出现“和为
如果实验继续进行下去,出现“和为![]() ”的频率将稳定在它的概率附近.试估计出现“和为
”的频率将稳定在它的概率附近.试估计出现“和为![]() ”的概率;
”的概率;
![]() 根据
根据![]() 中结论,求出自然数
中结论,求出自然数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com