
【题目】如图,点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 在
在![]() 上,
上,![]() 于点
于点![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 延长线上一点,且
延长线上一点,且![]() ,
,![]() .
.

![]() 求证:
求证:![]() 是
是![]() 的切线;
的切线;
![]() 若点
若点![]() 是弧
是弧![]() 的中点,且
的中点,且![]() 交
交![]() 于点
于点![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析(2)![]()
【解析】
(1)连结AC,先求得AC是直径,从而求得∠D=∠ACB,根据已知得出AB=6,然后根据勾股定理求得AC,根据勾股定理逆定理证得∠CAH=90°即CA⊥AH,即可证得结论;
(2)由点D是弧CE的中点,得出∠EAD=∠DAC,进而求得∠EAH=∠HCA,然后求得∠AFH=∠HAF,根据等角对等边得出HF=HA=![]() ,最后根据射影定理得出AH2=EHCH,即可求得EH的值,进而求得EF的值.
,最后根据射影定理得出AH2=EHCH,即可求得EH的值,进而求得EF的值.
![]() 证明:连结
证明:连结![]() ,
,
∵![]() 于点
于点![]() ,
,
∴![]() 是
是![]() 的直径,
的直径,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
由勾股定理![]() ,
,
在![]() 中,由勾股定理逆定理:
中,由勾股定理逆定理:![]() ,
,
∴![]() 即
即![]() ,
,
∴![]() 是
是![]() 的切线.
的切线.

![]() 解:∵点
解:∵点![]() 是弧
是弧![]() 的中点,
的中点,
∴![]() ,
,
∵![]() 是
是![]() 的直径,
的直径,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() 可得
可得![]() ,
,
∴![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为

A、2 B、2.5或3.5 C、3.5或4.5 D、2或3.5或4.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】合肥地铁一号线的开通运行给合肥市民出行方式带来了一些变化,小朱和小张准备利用课余时间,以问卷的分式对合肥市民的出行方式进行调查,如图是合肥地铁一号线图(部分),小朱和小张分别从塘西河公园站(用A表示)、金斗公园站(用B表示)、云谷路站(用C表示)、万达城站(用D表示)这四站中,随机选取一站作为调查的站点.

(1)在这四站中,小朱选取问卷调查的站点是万达城站的概率是多少?
(2)求小朱选取问卷调查的站点与小张选取问卷调查的站点相邻的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B两个村庄的坐标分别为(2,2)、(7,4),一辆汽车从原点O出发,在x轴上行驶.
(1)汽车行驶到什么位置时离村庄A最近?写出此位置的坐标.
(2)汽车行驶到什么位置时离村庄B最近?写出此位置的坐标.
(3)请在图中画出汽车到两村庄的距离和最短的位置,并求出此最短的距离和.

查看答案和解析>>
科目:初中数学 来源: 题型:
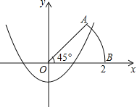
【题目】如图,以扇形![]() 的顶点
的顶点![]() 为原点,半径
为原点,半径![]() 所在的直线为
所在的直线为![]() 轴,建立平面直角坐标系,点
轴,建立平面直角坐标系,点![]() 的坐标为
的坐标为![]() ,
,![]() .现从
.现从![]() 中随机选取一个数记为
中随机选取一个数记为![]() ,则
,则![]() 的值既使得抛物线
的值既使得抛物线![]() 与扇形
与扇形![]() 的边界有公共点,又使得关于
的边界有公共点,又使得关于![]() 的方程
的方程![]() 的解是正数的概率是________.
的解是正数的概率是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是 ( )

A. ![]() B. 2
B. 2![]() C. 3 D. 2
C. 3 D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车4S店销售某种型号的汽车,每辆进货价为15万元,该店经过一段时间的市场调研发现:当销售价为25万元时,平均每周能售出8辆,而当销售价每降低0.5万元时,平均每周能多售出1辆.该4S店要想平均每周的销售利润为90万元,并且使成本尽可能的低,则每辆汽车的定价应为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O是坐标原点,菱形OABC的顶点A(3,4),C在x轴的负半轴,抛物线y=﹣![]() (x﹣2)2+k过点A.
(x﹣2)2+k过点A.
(1)求k的值;
(2)若把抛物线y=﹣![]() (x﹣2)2+k沿x轴向左平移m个单位长度,使得平移后的抛物线经过菱形OABC的顶点C.试判断点B是否落在平移后的抛物线上,并说明理由.
(x﹣2)2+k沿x轴向左平移m个单位长度,使得平移后的抛物线经过菱形OABC的顶点C.试判断点B是否落在平移后的抛物线上,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com