
| A. | $\frac{3\sqrt{3}}{2}$ | B. | $\frac{3\sqrt{3}}{4}$ | C. | 2-$\sqrt{3}$ | D. | 1+$\sqrt{3}$ |
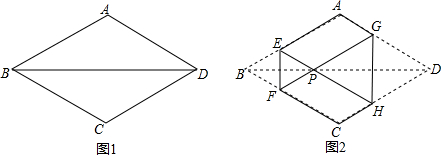
分析 由六边形AEFCHG面积=菱形ABCD的面积-△EBF的面积-△GDH的面积.得出函数关系式,进而求出最大值.
解答 解:六边形AEFCHG面积=菱形ABCD的面积-△EBF的面积-△GDH的面积.
∵菱形纸片ABCD的边长为2,∠ABC=60°,
∴AC=2,
∴BD=2$\sqrt{3}$,
∴S菱形ABCD=$\frac{1}{2}$AC•BD=$\frac{1}{2}×$2×2$\sqrt{3}$=2$\sqrt{3}$,
设AE=x,
则六边形AEFCHG面积=2$\sqrt{3}$-$\frac{1}{2}$×(2-x)•$\frac{\sqrt{3}}{2}$(2-x)-$\frac{1}{2}$x•$\frac{\sqrt{3}}{2}$x
=-$\frac{\sqrt{3}}{2}$x2+$\sqrt{3}$x+$\sqrt{3}$
=-$\frac{\sqrt{3}}{2}$(x-1)2+$\frac{3}{2}$$\sqrt{3}$,
∴六边形AEFCHG面积的最大值是$\frac{3}{2}$$\sqrt{3}$.
故选A.
点评 考查了翻折变换(折叠问题),二次函数最值问题,本题关键是设出未知数表示六边形面积,把图形问题转化为函数问题,有一定的难度.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
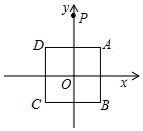 如图,在平面直角坐标系中,正方形ABCD的顶点A(1,1),B(1,-1),C(-1,-1),D(-1,1),y轴上有一点P(0,2),作点P关于点A的对称点P1,作点P1关于点B的对称点P2,作点P2关于点C的对称点P3,作点P3关于点D的对称点P4,作点P4关于点A的对称点P5,作点P5关于点B的对称点P6,…,按此规律操作下去,则点P2017的坐标为( )
如图,在平面直角坐标系中,正方形ABCD的顶点A(1,1),B(1,-1),C(-1,-1),D(-1,1),y轴上有一点P(0,2),作点P关于点A的对称点P1,作点P1关于点B的对称点P2,作点P2关于点C的对称点P3,作点P3关于点D的对称点P4,作点P4关于点A的对称点P5,作点P5关于点B的对称点P6,…,按此规律操作下去,则点P2017的坐标为( )| A. | (2,0) | B. | (0,2) | C. | (0,-2) | D. | (-2,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -4955 | B. | 4955 | C. | -4950 | D. | 4950 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
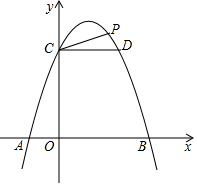 二次函数y=-x2+2x+3的图象与x轴交于A,B两点(点A在B的左侧),与y轴交于点C,过点C作y轴的垂线交抛物线于另一点D.
二次函数y=-x2+2x+3的图象与x轴交于A,B两点(点A在B的左侧),与y轴交于点C,过点C作y轴的垂线交抛物线于另一点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
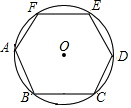 正六边形ABCDEF内接于⊙O,正六边形的周长是12,则⊙O的半径是( )
正六边形ABCDEF内接于⊙O,正六边形的周长是12,则⊙O的半径是( )| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com