
【题目】如图,△ABC中,AB=AC,点D为BC上一点,且AD=DC,过A,B,D三点作⊙O,AE是⊙O的直径,连结DE. 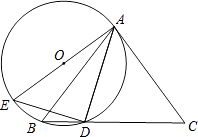
(1)求证:AC是⊙O的切线;
(2)若sinC= ![]() ,AC=6,求⊙O的直径.
,AC=6,求⊙O的直径.
【答案】
(1)证明:∵AB=AC,AD=DC,
∴∠C=∠B,∠1=∠C,
∴∠1=∠B,
又∵∠E=∠B,
∴∠1=∠E,
∵AE是⊙O的直径,
∴∠ADE=90°,
∴∠E+∠EAD=90°,
∴∠1+∠EAD=90°,即∠EAC=90°,
∴AE⊥AC,
∴AC是⊙O的切线
(2)解:过点D作DF⊥AC于点F,如图,
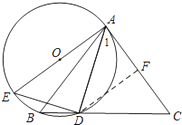
∵DA=DC,
∴CF= ![]() AC=3,
AC=3,
在Rt△CDF中,∵sinC= ![]() =
= ![]() ,
,
设DF=4x,DC=5x,
∴CF= ![]() =3x,
=3x,
∴3x=3,解得x=1,
∴DC=5,
∴AD=5,
∵∠ADE=∠DFC=90°,∠E=∠C,
∴△ADE∽△DFC,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得AE=
,解得AE= ![]() ,
,
即⊙O的直径为 ![]() .
.
【解析】(1)根据等腰三角形的性质,由AB=AC,AD=DC得∠C=∠B,∠1=∠C,则∠1=∠B,根据圆周角定理得∠E=∠B,∠ADE=90°,所以∠1+∠EAD=90°,然后根据切线的判定定理即可得到AC是⊙O的切线;(2)过点D作DF⊥AC于点F,如图,根据等腰三角形的性质得CF= ![]() AC=3,在Rt△CDF中,利用正弦定义得sinC=
AC=3,在Rt△CDF中,利用正弦定义得sinC= ![]() =
= ![]() ,则设DF=4x,DC=5x,利用勾股定理得CF=3x,所以3x=3,解得x=1,于是得到DC=AD=5,然后证明△ADE∽△DFC,再利用相似比可计算AE即可.
,则设DF=4x,DC=5x,利用勾股定理得CF=3x,所以3x=3,解得x=1,于是得到DC=AD=5,然后证明△ADE∽△DFC,再利用相似比可计算AE即可.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,平行四边形 ABCD 中,AD∥BC,AB=BC=CD=AD=4,∠A=∠C=60°,连接 BD,将△BCD 绕点 B 旋转,当 BD(即 BD′)与 AD 交于一点 E,BC(即 BC′)同时与 CD 交于一点 F 时,下列结论正确的是( )
①AE=DF;②∠BEF=60°;③∠DEB=∠DFB;④△DEF 的周长的最小值是4+2![]()
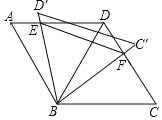
A. ①② B. ②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB的解析式为y=![]() x+4,与y轴交于点A,与x轴交于点B,点P为线段AB上的一个动点,作PE⊥y轴于点E,PF⊥x轴于点F,连接EF,则线段EF的最小值为_____.
x+4,与y轴交于点A,与x轴交于点B,点P为线段AB上的一个动点,作PE⊥y轴于点E,PF⊥x轴于点F,连接EF,则线段EF的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有分别标有汉字“幸”、“福”、“聊”、“城”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,球上的汉字刚好是“福”的概率为多少?
(2)小颖从中任取一球,记下汉字后放回袋中,然后再从中任取一球,求小颖取出的两个球上汉字恰能组成“幸福”或“聊城”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】结合数轴与绝对值的知识回答下列问题:
(1)数轴上表示4和1的两点之间的距离是 ;表示﹣3和2两点之间的距离是 ;一般地,数轴上表示数m和数n的两点之间的距离等于|m﹣n|.如果表示数a和﹣2的两点之间的距离是3,那么a= ;
(2)若数轴上表示数a的点位于﹣4与2之间,求|a+4|+|a﹣2|的值;
(3)当a取何值时,|a+5|+|a﹣1|+|a﹣4|的值最小,最小值是多少?请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场去年计划生产玉米和小麦共200吨.采用新技术后,实际产量为225吨,其中玉米超产5%,小麦超产15%.该农场去年实际生产玉米、小麦各多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交于BE的延长线于点F,且AF=DC,连接CF. 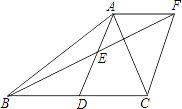
(1)求证:D是BC的中点;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com