
【题目】如图,直线AB的解析式为y=![]() x+4,与y轴交于点A,与x轴交于点B,点P为线段AB上的一个动点,作PE⊥y轴于点E,PF⊥x轴于点F,连接EF,则线段EF的最小值为_____.
x+4,与y轴交于点A,与x轴交于点B,点P为线段AB上的一个动点,作PE⊥y轴于点E,PF⊥x轴于点F,连接EF,则线段EF的最小值为_____.

【答案】![]()
【解析】
在一次函数y=![]() x+4中,分别令x=0, y=0,解相应方程,可求得A、B两点的坐标,由矩形的性质可知EF=OP,可知当OP最小时,则EF有最小值,由垂线段最短可知当OP⊥AB时,满足条件,根据直角三角形面积的不同表示方法可求得OP的长,即可求得EF的最小值.
x+4中,分别令x=0, y=0,解相应方程,可求得A、B两点的坐标,由矩形的性质可知EF=OP,可知当OP最小时,则EF有最小值,由垂线段最短可知当OP⊥AB时,满足条件,根据直角三角形面积的不同表示方法可求得OP的长,即可求得EF的最小值.
∵一次函数y=![]() x+4中,令x=0,则y=4,令y=0,则x=-3,
x+4中,令x=0,则y=4,令y=0,则x=-3,
∴A(0,4),B(-3,0),
∵PE⊥y轴于点E,PF⊥x轴于点F,
∴四边形PEOF是矩形,且EF=OP,
∵O为定点,P在线段上AB运动,
∴当OP⊥AB时,OP取得最小值,此时EF最小,
∵A(0,4),点B坐标为(-3,0),
∴OA=4,OB=3,
由勾股定理得:AB=![]() =5,
=5,
∵AB·OP=AO·BO=2S△OAB,
∴OP=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图像与反比例函数y= ![]() 的图像交于点A﹙﹣2,﹣5﹚C﹙5,n﹚,交y轴于点B,交x轴于点D.
的图像交于点A﹙﹣2,﹣5﹚C﹙5,n﹚,交y轴于点B,交x轴于点D. 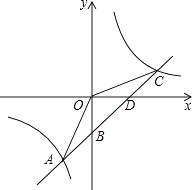
(1)求反比例函数y= ![]() 和一次函数y=kx+b的表达式;
和一次函数y=kx+b的表达式;
(2)连接OA,OC.求△AOC的面积.、
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买5千克这种苹果比分五次购买1千克这种苹果可节省( )元.

A. 4 B. 5 C. 6 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购买60件A商品和30件B商品共用了1080元,购买50件A商品和20件B商品共用了880元.
(1)A、B两种商品的单价分别是多少元?
(2)已知该商店购买B商品的件数比购买A商品的件数的2倍少4件,如果需要购买A、B两种商品的总件数不少于32件,且该商店购买的A、B两种商品的总费用不超过296元,那么该商店有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
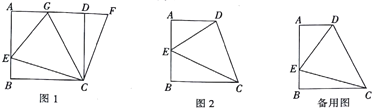
【题目】如图1,在正方形ABCD中,点E是AB上一点,点F是AD延长线上一点,且DF=BE,连接CE、CF.
(1)求证:CE=CF.
(2)在图1中,若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
(3)根据你所学的知识,运用(1)、(2)解答中积累的经验,完成下列各题,如图2,在四边形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,且∠DCE=45°.
①若AE=6,DE=10,求AB的长;
②若AB=BC=9,BE=3,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,点D为BC上一点,且AD=DC,过A,B,D三点作⊙O,AE是⊙O的直径,连结DE. 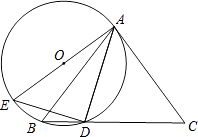
(1)求证:AC是⊙O的切线;
(2)若sinC= ![]() ,AC=6,求⊙O的直径.
,AC=6,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
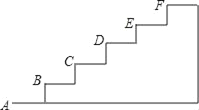
【题目】如图是某台阶的一部分,如果A点的坐标为(0,0),B点的坐标为(1,1),
(1)请建立适当的直角坐标系,并写出其余各点的坐标;
(2)如果台阶有10级,请你求出该台阶的长度和高度;
(3)若这10级台阶的宽度都是2m,单位长度为1m,现要将这些台阶铺上地毯,需要多少平方米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com