
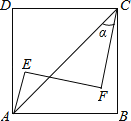
【题目】如图,正方形ABCD内有两点E、F满足AE=4,tanα=![]() ,AE⊥EF,CF⊥EF,EF=CF,则正方形的边长为 .
,AE⊥EF,CF⊥EF,EF=CF,则正方形的边长为 .
【答案】10![]() .
.
【解析】
试题分析:由AE⊥EF,CF⊥EF,AE=4,tanα=![]() ,可找出ME的长度以及用CF表示出FM的长度,再由EF=CF,可找出CF的长,结合勾股定理与正方形的性质即可得出正方形的边长.
,可找出ME的长度以及用CF表示出FM的长度,再由EF=CF,可找出CF的长,结合勾股定理与正方形的性质即可得出正方形的边长.
解:令EF与AC的交点为点M,如图所示.

∵AE⊥EF,CF⊥EF,
∴∠AEM=∠CFM=90°,
∵∠AME=∠CMF,
∴△AME∽CMF,
∴∠EAM=∠FCM=α.
∵AE=4,tanα=![]() ,
,
∴EM=3,FM=![]() CF,
CF,
∵EF=EM+FM=3+![]() CF=CF,
CF=CF,
∴CF=12,FM=9.
由勾股定理可知:AM=![]() =5,CM=
=5,CM=![]() =15,
=15,
∴AC=AM+CM=20.
∵四边形ABCD为正方形,
∴AB=![]() AC=10
AC=10![]() .
.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】我们把三角形中最大内角与最小内角的度数差称为该三角形的“内角正度值”.如果等腰三角形的“内角正度值”为45°,那么该等腰三角形的顶角等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(m+6)x+3m+9=0的两个实数根分别为x1,x2.
(1)求证:该一元二次方程总有两个实数根;
(2)若n=x1+x2﹣5,判断动点P(m,n)所形成的函数图象是否经过点A(4,5),并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,①锐角都相等;②大于90°且小于平角的角是钝角;③互为相反数的两数和为0;④若l1⊥l2,l1⊥l3,则l2⊥l3.其中正确的有( )
A. ①② B. ②③ C. ③④ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:31=3,32=9,33=27,34=81,35=243,36=729,37=2187,…, 则32018的末位数字是( )
A. 9 B. 1 C. 3 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好地宣传“开车不喝酒,喝酒不开车”的驾车理念,江南晚报社设计了如下的调查问卷(单选).
克服酒驾--你认为哪一种方式更好?
A.司机酒驾,乘客有责,让乘客帮助监督
B.车上张贴“请勿酒驾”的提醒标志
C.签订““永不酒驾”保证书
D.希望交警加大检查力度
E.查出酒驾,追究就餐饭店的连带责任
在随机调查了本市全部3000名司机中的部分司机后,整理相关数据并制作了两个不完整的统计图:

根据以上信息解答下列问题:
(1)请补全条形统计图,并直接写出扇形统计图中m= ;
(2)该市支持选项D的司机大约有多少人?
(3)若要从该市支持选项B的司机中随机抽取90名,给他们发放“请勿酒驾”的提醒标志,则支持该选项的司机小李被抽中的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com