
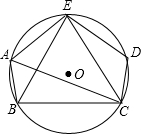
 如图,△ABC是⊙O的内接三角形,点D,E在⊙O上,连接AE,DE,CD,BE,CE,∠EAC+∠BAE=180°,$\widehat{AB}$=$\widehat{CD}$.
如图,△ABC是⊙O的内接三角形,点D,E在⊙O上,连接AE,DE,CD,BE,CE,∠EAC+∠BAE=180°,$\widehat{AB}$=$\widehat{CD}$.分析 (1)由A、B、C、E四点共圆的性质得:∠BCE+∠BAE=180°,则∠BCE=∠EAC,所以$\widehat{BE}$=$\widehat{CE}$,则弦相等;
(2)根据SSS证明△ABE≌△DCE;
(3)作BC和BE两弦的弦心距,证明Rt△GBO≌Rt△HBO(HL),则∠OBH=30°,设OH=x,则OB=2x,根据勾股定理列方程求出x的值,可得半径的长.
解答 (1)解:BE=CE,
理由:∵∠EAC+∠BAE=180°,∠BCE+∠BAE=180°,
∴∠BCE=∠EAC,
∴$\widehat{BE}$=$\widehat{CE}$,
∴BE=CE;
(2)证明:∵$\widehat{AB}=\widehat{CD}$,
∴AB=CD,
∵$\widehat{BE}$=$\widehat{CE}$,
∴$\widehat{AE}=\widehat{ED}$,
∴AE=ED,
由(1)得:BE=CE,
在△ABE和△DCE中,
∵$\left\{\begin{array}{l}{AE=DE}\\{AB=CD}\\{BE=CE}\end{array}\right.$,
∴△ABE≌△DCE(SSS);
(3)解:如图,∵过O作OG⊥BE于G,OH⊥BC于H,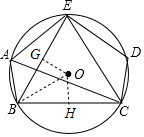
∴BH=$\frac{1}{2}$BC=$\frac{1}{2}$×8=4,
BG=$\frac{1}{2}$BE,
∵BE=CE,∠EBC=∠EAC=60°,
∴△BEC是等边三角形,
∴BE=BC,
∴BH=BG,
∵OB=OB,
∴Rt△GBO≌Rt△HBO(HL),
∴∠OBH=∠GBO=$\frac{1}{2}$∠EBC=30°,
设OH=x,则OB=2x,
由勾股定理得:(2x)2=x2+42,
x=$\frac{4\sqrt{3}}{3}$,
∴OB=2x=$\frac{8\sqrt{3}}{3}$,
∴⊙O的半径为$\frac{8\sqrt{3}}{3}$.
点评 本题是圆的综合题,考查了四点共圆的性质、三角形全等的性质和判定、勾股定理、直角三角形30°的性质,难度适中,第一问还可以利用三角形全等得出对应边相等得结论;第三问作辅助线,利用勾股定理列方程是关键.


 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
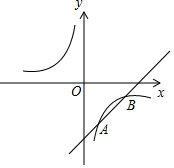 如图,已知一次函数y=kx+b与反比例函数y=$\frac{m}{x}$交于A(1,-3),B(a,-1)两点.
如图,已知一次函数y=kx+b与反比例函数y=$\frac{m}{x}$交于A(1,-3),B(a,-1)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
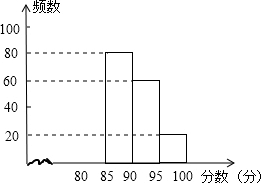 某校组织了一次G20知识竞赛活动,根据获奖同学在竞赛中的成绩制成的统计图表如下,仔细阅读图表解答问题:
某校组织了一次G20知识竞赛活动,根据获奖同学在竞赛中的成绩制成的统计图表如下,仔细阅读图表解答问题:| 分数段 | 频数 | 频率 |
| 80≤x<85 | a | 0.2 |
| 85≤x<90 | 80 | b |
| 90≤x<95 | 60 | c |
| 95≤x<100 | 20 | 0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com