
 在四边形纸片ABCD中,∠A=70°,∠B=80°.现将纸片的一角对折,使点C落在△ABC内,若∠1=30°,则∠2的度数为
在四边形纸片ABCD中,∠A=70°,∠B=80°.现将纸片的一角对折,使点C落在△ABC内,若∠1=30°,则∠2的度数为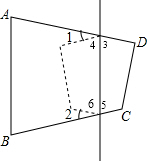 根据题意得∠3=∠4,∠5=∠6,
根据题意得∠3=∠4,∠5=∠6,

科目:初中数学 来源: 题型:
 如图,在四边形纸片ABCD中,AD∥BC,AB∥CD,将纸片折叠,点A、D分别落在A′、D′处,且A′D′经过点B,EF为折痕,若∠D′FC=86°时,∠A′EB=( )
如图,在四边形纸片ABCD中,AD∥BC,AB∥CD,将纸片折叠,点A、D分别落在A′、D′处,且A′D′经过点B,EF为折痕,若∠D′FC=86°时,∠A′EB=( )查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2011-2012学年江西九江七年级第二学期期中联考数学试卷(带解析) 题型:解答题
如图,在四边形纸片ABCD中,已知:AD∥BC,AB∥CD,∠B=90°,现将四边形纸片ABCD对折,折痕为PF(点P在BC上,点F在DC上),使顶点C落在四边形ABCD内一点C′,PC′的延长线交AD于M,再将纸片的另一部分对折(折痕为ME),使顶点A落在直线PM上一点A′.
(1)填空:
因为AD∥BC,(已知)
所以∠B+∠A=180°( )
又因为∠B=90°(已知)
所以∠A= 度.
则:∠EA′M= 度.
又因为AB∥CD(已知)
同理:∠FC′P=∠C= 度.
所以∠EA′M ∠FC′P(填 “<”或“=”或“>”)
所以 ∥ 理由:( ).
(2)ME与PF平行吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014届江西九江七年级第二学期期中联考数学试卷(解析版) 题型:解答题
如图,在四边形纸片ABCD中,已知:AD∥BC,AB∥CD,∠B=90°,现将四边形纸片ABCD对折,折痕为PF(点P在BC上,点F在DC上),使顶点C落在四边形ABCD内一点C′,PC′的延长线交AD于M,再将纸片的另一部分对折(折痕为ME),使顶点A落在直线PM上一点A′.

(1)填空:
因为AD∥BC,(已知)
所以∠B+∠A=180°( )
又因为∠B=90°(已知)
所以∠A= 度.
则:∠EA′M= 度.
又因为AB∥CD(已知)
同理:∠FC′P=∠C= 度.
所以∠EA′M ∠FC′P(填 “<”或“=”或“>”)
所以 ∥ 理由:( ).
(2)ME与PF平行吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com