
分析 (1)纵坐标为0,横坐标为0,将其直接代入二次函数y=$\frac{1}{2}$(x-5)(x+m)即可求得坐标.
(2)①求p的值,通常利用表达式表示p,此时p恰为不含字母的式子.因为t=2,此时p=yN-yM,这里yM为点M的纵坐标,yN为点N的纵坐标;
②求最值也要首先表示p,不过发现因为C为抛物线与直线的交点,在-m≤t≤0,p=yM-yN,当0≤t≤5时,p=yN-yM.如此要分开讨论最值,然后再综合在一起,讨论时不要遗漏题目中关于m的限制:0<m≤1.
解答 解:(1)令y=0,得$\frac{1}{2}$(x-5)(x+m)=0,
解得x1=5,x2=-m,
∵m>0,
∴-m<0,
∵点A在点B的右侧,
∴A(5,0),B(-m,0),
令x=0,得y=-$\frac{5}{2}$m,
∴C(0,-$\frac{5}{2}$m);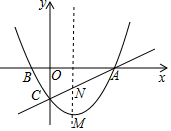 (2)①设AC的函数关系式为y=kx-$\frac{5}{2}$m,
(2)①设AC的函数关系式为y=kx-$\frac{5}{2}$m,
把A(5,0)代入y=kx-$\frac{5}{2}$m,解得k=$\frac{1}{2}$m,
∴y=$\frac{1}{2}$mx-$\frac{5}{2}$m,
∵t=2,
∴点M的纵坐标为yM=$\frac{1}{2}$(2-5)(2+m)=-$\frac{3}{2}$(2+m),
点N的纵坐标为yN=$\frac{1}{2}$m×2-$\frac{5}{2}$m=-$\frac{3}{2}$m,
∴p=yN-yM=-$\frac{3}{2}$m+$\frac{3}{2}$(2+m)=3;
②∵点M的横坐标为t,
∴点M的纵坐标为yM=$\frac{1}{2}$(t-5)(t+m)=$\frac{1}{2}$t2+$\frac{1}{2}$(m-5)t-$\frac{5}{2}$m,
点N的纵坐标为yN=$\frac{1}{2}$mt-$\frac{5}{2}$m,
当0≤t≤5时,p=yN-yM=-$\frac{1}{2}$t2+$\frac{5}{2}$t=-$\frac{1}{2}$(t-$\frac{5}{2}$)2+$\frac{25}{8}$,
当t=$\frac{5}{2}$时,p取得最大值$\frac{25}{8}$,
当-m≤t<0时,p=yM-yN=$\frac{1}{2}$t2-$\frac{5}{2}$t=$\frac{1}{2}$(t-$\frac{5}{2}$)2-$\frac{25}{8}$,
此二次函数图象开口向上,对称轴为直线t=$\frac{5}{2}$,
∴在-m≤t<0时,p随t的增大而减少,
∴当t=-m时,p取得最大值为$\frac{1}{2}$m2+$\frac{5}{2}$m,
设w=$\frac{1}{2}$m2+$\frac{5}{2}$m,
m=-$\frac{5}{2}$m为对称轴,
∴0<m≤1时,w的值随m的增大而增大,
∴m=1时,w最大值为3,
∵3<$\frac{25}{8}$m,
∴当t=$\frac{5}{2}$时,p取得最大值为$\frac{25}{8}$.
点评 本题考查了二次函数的性质,并且设置了多次最值问题的讨论,是一道很需要基本功的题目.但是本题思路及方法都属于常规套路,综上是一道质量很高的题目.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | 3 | D. | -3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
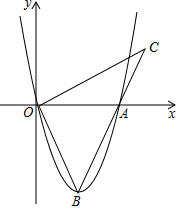 如图,抛物线y=ax2-4x的图象与x轴的一个交点为A(6,0),点B为抛物线的顶点,连结OB、AB,作OC⊥OB交BA的延长线于点C.
如图,抛物线y=ax2-4x的图象与x轴的一个交点为A(6,0),点B为抛物线的顶点,连结OB、AB,作OC⊥OB交BA的延长线于点C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
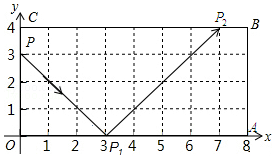 如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时,记为点P1,第2次碰到矩形的边时,记为点P2,…第n次碰到矩形的边时,记为点Pn,则点P4的坐标是(5,0);点P125的坐标是(1,4).
如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时,记为点P1,第2次碰到矩形的边时,记为点P2,…第n次碰到矩形的边时,记为点Pn,则点P4的坐标是(5,0);点P125的坐标是(1,4).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{n}{n+3}$ | B. | $\frac{1}{n+3}$ | C. | $\frac{n}{2n+3}$ | D. | $\frac{1}{n}$+$\frac{1}{n+3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买5千克这种苹果比分五次购买1千克这种苹果可节省( )元.
如图,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买5千克这种苹果比分五次购买1千克这种苹果可节省( )元.| A. | 6 | B. | 8 | C. | 9 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
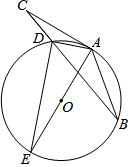 如图,在△ABC中,点D为BC上一点,过A,B,D三点作⊙O,AE是⊙O的直径,AC是⊙O的切线,AD=DC,连结DE.
如图,在△ABC中,点D为BC上一点,过A,B,D三点作⊙O,AE是⊙O的直径,AC是⊙O的切线,AD=DC,连结DE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2ab)•(-3ab)3=-54a4b4 | B. | 5x2•(3x3)2=15x12 | ||
| C. | (-0.1b)•(-10b2)3=-b7 | D. | (3×10n)($\frac{1}{3}$×10n)=102n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com