
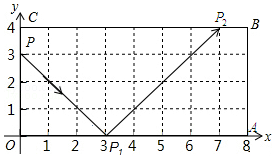
 如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时,记为点P1,第2次碰到矩形的边时,记为点P2,…第n次碰到矩形的边时,记为点Pn,则点P4的坐标是(5,0);点P125的坐标是(1,4).
如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时,记为点P1,第2次碰到矩形的边时,记为点P2,…第n次碰到矩形的边时,记为点Pn,则点P4的坐标是(5,0);点P125的坐标是(1,4). 科目:初中数学 来源: 题型:解答题
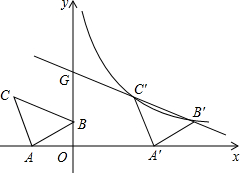 如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0),B(0,1).
如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0),B(0,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
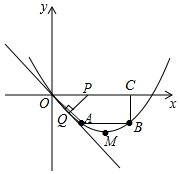 已知:如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C,A(2,-2),B(6,-2),动点P从点O出发,沿着x轴正方向以每秒2个单位的速度移动,过点P作PQ垂直于直线OA,垂足为点Q,设点P移动的时间t秒(0<t<4).△OPQ与四边形OABC重叠部分的面积为S.
已知:如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C,A(2,-2),B(6,-2),动点P从点O出发,沿着x轴正方向以每秒2个单位的速度移动,过点P作PQ垂直于直线OA,垂足为点Q,设点P移动的时间t秒(0<t<4).△OPQ与四边形OABC重叠部分的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
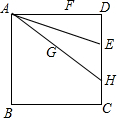 如图,正方形ABCD的边长为6,E,F分别是边CD和AD上的点,且DF=DE=2,连结AE,作点F关于AE的对称点G,连结AG并延长交CD于点H,过点G的直线l分别交线段AF,BC于点M,N,且MN=AH.则AH和MF的长分别是$\frac{15}{2}$和$\frac{13}{5}$.
如图,正方形ABCD的边长为6,E,F分别是边CD和AD上的点,且DF=DE=2,连结AE,作点F关于AE的对称点G,连结AG并延长交CD于点H,过点G的直线l分别交线段AF,BC于点M,N,且MN=AH.则AH和MF的长分别是$\frac{15}{2}$和$\frac{13}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2-y2=(x-y)2 | B. | a2+a+1=(a+1)2 | ||
| C. | 2xy-6x=2x(y-3) | D. | a2+4a+21=a(a+4)+21 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
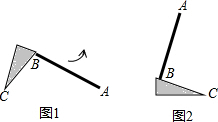 如图1,教室里有一只倒地的装垃圾的灰斗,BC与地面的夹角为50°,∠C=25°,小贤同学将它绕点C旋转一定角度,扶起平放在地面上(如图2),则灰斗柄AB绕点C转动的角度为( )
如图1,教室里有一只倒地的装垃圾的灰斗,BC与地面的夹角为50°,∠C=25°,小贤同学将它绕点C旋转一定角度,扶起平放在地面上(如图2),则灰斗柄AB绕点C转动的角度为( )| A. | 75° | B. | 25° | C. | 115° | D. | 105° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com