
问题:如图1,在正方形ABCD内有一点P,PA=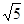 ,PB=
,PB=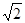 ,PC=1,求∠BPC的角度.
,PC=1,求∠BPC的角度.
分析:根据已知条件比较分散的特点,我们可以通过旋转变换,将分散的已知条件集中在一起,于是将△BPC绕点B逆时针旋转900,得到了△BP1A(如图2),然后连接PP1.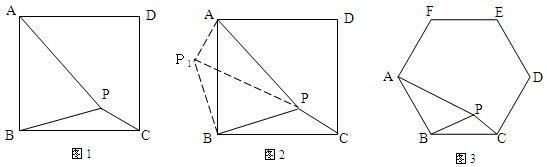
解决问题:请你通过计算求出图2中∠BPC的角度;
类比研究:如图3,若在正六边形ABCDEF内有一点P,且PA=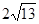 ,PB=4,PC=2.
,PB=4,PC=2.
(1)请你通过计算求出∠BPC的度数;
(2)直接写出正六边形ABCDEF的边长为 .
解决问题1350;类比研究(1)1200;(2)2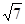
解析试题分析:(1)根据旋转的性质得到∠P′BP=90°,BP′=BP=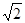 ,P′A=PC=1,∠BP′A=∠BPC,则△BPP′为等腰直角三角形,根据等腰直角三角形的性质得PP′=
,P′A=PC=1,∠BP′A=∠BPC,则△BPP′为等腰直角三角形,根据等腰直角三角形的性质得PP′=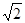 PB=2,∠BP′P=45°,利用勾股定理的逆定理可得到△APP′为直角三角形,且∠AP′P=90°,则∠BPC=∠BP′A=45°+90°=135°;
PB=2,∠BP′P=45°,利用勾股定理的逆定理可得到△APP′为直角三角形,且∠AP′P=90°,则∠BPC=∠BP′A=45°+90°=135°;
(2)把△BPC绕点B逆时针旋转120°,得到了△BP′A,根据旋转的性质得到∠P′BP=120°,BP′=BP=4,P′A=PC=2,∠BP′A=∠BPC,则∠BP′P=∠BPP′=30°,得到P′H=PH,利用含30°的直角三角形三边的关系得到BH=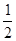 BP′=2,P′H=
BP′=2,P′H= BH=2
BH=2 ,得到P′P=2P′H=4
,得到P′P=2P′H=4 ,再利用勾股定理的逆定理可得到△APP′为直角三角形,且∠AP′P=90°,于是有∠BPC=∠BP′A=30°+90°=120°;过A作AG⊥BP′于G点,利用含30°的直角三角形三边的关系得到GP′=
,再利用勾股定理的逆定理可得到△APP′为直角三角形,且∠AP′P=90°,于是有∠BPC=∠BP′A=30°+90°=120°;过A作AG⊥BP′于G点,利用含30°的直角三角形三边的关系得到GP′=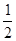 AP′=1,AG=
AP′=1,AG= GP′=
GP′= ,然后在Rt△AGB中利用勾股定理即可计算出AB长.
,然后在Rt△AGB中利用勾股定理即可计算出AB长.
(1)∵△BPC绕点B逆时针旋转90°,得到了△BP′A,
∴∠P′BP=90°,BP′=BP=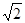 ,P′A=PC=1,∠BP′A=∠BPC,
,P′A=PC=1,∠BP′A=∠BPC,
∴△BPP′为等腰直角三角形,
∴PP′=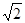 PB=2,∠BP′P=45°,
PB=2,∠BP′P=45°,
在△APP′中,AP=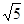 ,PP′=2,AP′=1,
,PP′=2,AP′=1,
∵(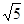 )2=22+12,
)2=22+12,
∴AP2=PP′2+AP′2,
∴△APP′为直角三角形,且∠AP′P=90°
∴∠BP′A=45°+90°=135°,
∴∠BPC=∠BP′A=135°;
(2)∵六边形ABCDEF为正六边形,
∴∠ABC=120°,
把△BPC绕点B逆时针旋转120°,得到了△BP′A,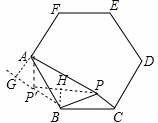
∴∠P′BP=120°,BP′=BP=4,P′A=PC=2,∠BP′A=∠BPC,
∴∠BP′P=∠BPP′=30°,
过B作BH⊥PP′于H,
∵BP′=BP,
∴P′H=PH,
在Rt△BP′H中,∠BP′H=30°,BP′=4,
∴BH=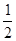 BP′=2,P′H=
BP′=2,P′H= BH=2
BH=2 ,
,
∴P′P=2P′H=4 ,
,
在△APP′中,AP=2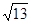 ,PP′=4
,PP′=4 ,AP′=2,
,AP′=2,
∵(2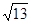 )2=(4
)2=(4 )2+22,
)2+22,
∴AP2=PP′2+AP′2,
∴△APP′为直角三角形,且∠AP′P=90°,
∴∠BP′A=30°+90°=120°,
∴∠BPC=120°,
过A作AG⊥BP′于G点,
∴∠AP′G=60°,
在Rt△AGP′中,AP′=2,∠GAP′=30°,
∴GP′=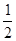 AP′=1,AG=
AP′=1,AG= GP′=
GP′= ,
,
在Rt△AGB中,GB=GP′+P′B=1+4=5,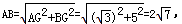
即正六边形ABCDEF的边长为2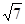 .
.
考点:旋转的性质,正方形的性质、等腰直角三角形的判定与性质、勾股定理与逆定理,含30°的直角三角形的性质
点评:解题的关键是熟记旋转的性质:旋转前后两图形全等,即对应角相等,对应线段相等;对应点与旋转中心的连线段的夹角等于旋转角.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:
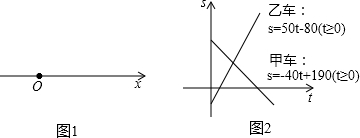
| 行驶方向 | 速度的大小(km/h) | 出发前的位置 | |
| 甲车 | |||
| 乙车 |
查看答案和解析>>
科目:初中数学 来源: 题型:



查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:学习周报 数学 华师大八年级版 2009-2010学年 第13期 总第169期 华师大版 题型:044
工具阅读:
在平面上画两条原点重合、互相垂直且具有相同单位长度的数轴(如图),这就建立了平面直角坐标系.通常把其中水平的一条数轴叫做x轴或横轴,取向右为正方向;铅直的数轴叫做y轴或纵轴,取向上为正方向;两数轴的交点O叫做坐标原点.

问题探究:如图1,在6×6的方格纸中,给出如下三种变换:P变换,Q变换,R变换.

将图形F沿x轴向右平移1格得图形F1,称为作1次P变换;
将图形F沿y轴翻折得图形F2,称为作1次Q变换;
将图形F绕坐标原点顺时针旋转90°得图形F3,称为作1次R变换.
规定:PQ变换表示先作1次Q变换,再作1次P变换;QP变换表示先作1次P变换,再作1次Q变换;Rn变换表示作n次R变换.
解答下列问题:
(1)作R4变换相当于至少作________次Q变换;
(2)请在图2中画出图形F作R2011变换后得到的图形F4;

(3)PQ变换与QP变换是否是相同的变换?请在图3中画出PQ变换后得到的图形F5,在图4中画出QP变换后得到的图形F6.

查看答案和解析>>
科目:初中数学 来源:同步题 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com