练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，分别连接正方形对边的中点，能将正方形划分成四个面积相等的小正方形用上述方法对一个边长为1的正方形进行划分，第1次划分得到图1，第2次划分图2，则第3次划分得到的图中共有______个正方形，借助划分得到的图形，计算的结果为______（用含的式子表示）

    【答案】4n+1

    【解析】

    （1）由第一次可得5个正方形，第二次可得9个正方形，第三次可得13个正方形，可得规律：第n次可得（4n+1）个正方形；

    （2）此题可看作上面几何体面积问题，即可求得答案．

    解：

    (1)∵第一次可得5个正方形，第二次可得9个正方形，第三次可得13个正方形，

    ∴第n次可得(4n+1)个正方形，

    (2)根据题意得：

    原式==；

    故答案为：（1）4n+1；（2）；

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】对于平面直角坐标系xOy中的任意两点M(x1，y1)，N(x2，y2)，给出如下定义：

    将|x1﹣x2|称为点M，N之间的“横长”，|y1﹣y2|称为点M，N之间的纵长”，点M与点N的“横长”与“纵长”之和称为“折线距离”，记作d(M，N)=|x1﹣x2|+|y1﹣y2|“．

    例如：若点M(﹣1，1)，点N(2，﹣2)，则点M与点N的“折线距离”为：d(M，N)=|﹣1﹣2|+|1﹣(﹣2)|=3+3=6．

    根据以上定义，解决下列问题：

    已知点P(3，2)．

    （1）若点A(a，2)，且d(P，A)=5，求a的值；

    （2）已知点B(b，b)，且d(P，B)＜3，直接写出b的取值范围；

    （3）若第一象限内的点T与点P的“横长”与“纵长”相等，且d(P，T)＞5，简要分析点T的横坐标t的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为丰富学生的课余生活，陶冶学生的情操，促进学生全面发展，某中学七年级开展了学生社团活动，学校为了解学生参加情况，对部分学生进行了调查，制作出如下的统计图：

    请根据统计图，完成以下问题：

    （1）这次共调查了 名学生；在扇形统计图中，表示“书法类”所在扇形的圆心角是 度．

    （2）请把统计图1 补充完整．

    （3）若七年级共有学生1100 名，请估算有多少名学生参加文学类社团．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，已知正比例函数与一次函数的图像交于点A.

    （1）求点A的坐标；

    （2）设x轴上一点P（a，b），过点P作x轴的垂线（垂线位于点A的右侧），分别交和的图像于点B、C，连接OC，若BC=OA，求△OBC的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们在学习《从面积到乘法公式》时，曾用两种不同的方法计算同一个图形的面积，探索了单项式乘多项式的运算法则：m（a+b+c）＝ma+mb+mc（如图1），多项式乘多项式的运算法则：

    （a+b）（c+d）＝ac+ad+bc+bd（如图2），以及完全平方公式：（a+b）2＝a2+2ab+b2（如图3）．

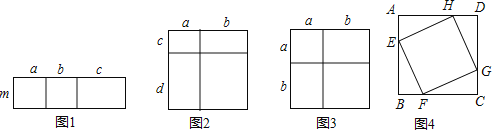
    把几个图形拼成一个新的图形，通过图形面积的计算，常常可以得到一些等式，这是研究数学问题的一种常用方法．

    （1）请设计两个图形说明一下两个等式成立（画出示意图，并标上字母）

    ①（a+b）（2a+b）＝2a2+3ab+b2

    ②（a+b+c）2＝a2+b2+c2+2ab+2ac+2bc

    （2）如图4，它是由四个形状、大小完全相同的直角三角形与中间的小正方形EFGH拼成的一个大正方形ABCD．如果每个直角三角形的较短的边长为a，较长的边长为b，最长的边长为c．试用两种不同的方法计算这个大正方形的面积，你能发现直角三角形的三边长a、b、c的什么数量关系？（注：写出解答过程）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学校在一次环保知识宣传活动中,需要印刷若干份调查问卷。印刷厂有甲、乙两种收费方式：甲种方式收制版费6元,每一份收印刷费0.1元；乙种方式不收制版费,每印一份收印刷费0.12元。设共印调查问卷份：

    (1)按甲种方式应收费多少元,按乙种方式应收费多少元(用含的代数式表示)；

    (2)若共需印刷500份调查问卷,通过计算说明选用哪种方式合算?

    (3)印刷多少份调查问卷时,甲、乙两种方式收费一样多?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：

    ①3x2﹣[2x2y﹣（xy﹣x2）]+4x2y

    ②×

    ③|﹣3|+（﹣1）2013×（π﹣3）0﹣

    ④[（3a+b）2﹣（2a﹣b）（﹣b﹣2a）]÷a

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，，作射线，再分别作上和的平分线、．

    (1) 如图①，当时，求的度数；

    (2) 如图②，当射线在内绕点旋转时，的大小是否发生变化，说明理由．

    (3) 当射线在外绕点旋转且为钝角时，画出图形，请直接写出相应的的度数(不必写出过程) ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知直线y=2x+1．

    （1）求已知直线与x轴、y轴的交点A、B的坐标；

    （2）若直线y=kx+b与已知直线关于y轴对称，求k与b的值．

    查看答案和解析>>

    同步练习册答案