
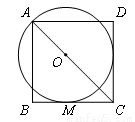
如图,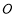 为正方形
为正方形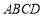 对角线AC上一点,以
对角线AC上一点,以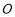 为圆心,
为圆心,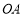 长为半径的⊙
长为半径的⊙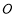 与
与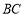 相切于点
相切于点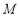 .
.
(1)求证: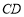 与⊙
与⊙ 相切;
相切;
(2)若⊙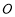 的半径为1,求正方形
的半径为1,求正方形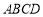 的边长.
的边长.
(1)证明见解析;(2)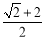 .
.
【解析】
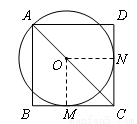
试题分析:(1)过O作ON⊥CD于N,连接OM,由切线的性质可知,OM⊥BC,再由AC是正方形ABCD的对角线可知AC是∠BCD的平分线,由角平分线的性质可知OM=ON,故CD与⊙O相切;
(2)先根据正方形的性质得出△MOC是等腰直角三角形,由勾股定理可求出OC的长,进而可求出AC的长,在Rt△ABC中,利用勾股定理即可求出AB的长.
试题解析:(1)【解析】
过O作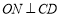 于N,连结OM,则
于N,连结OM,则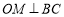 .
.
∵ AC是正方形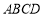 的对角线,
的对角线,
∴ AC是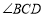 的平分线.
的平分线.
∴ OM=ON.
即圆心O到CD的距离等于⊙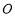 半径,
半径,
∴ 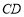 与⊙
与⊙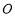 相切.
相切.
(2)由(1)易知 为等腰直角三角形,OM为半径,
为等腰直角三角形,OM为半径,
∴ OM=MC=1.
∴ 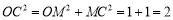 ,
,
∴ 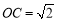 .
.
∴ 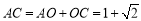
在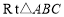 中,AB=BC,
中,AB=BC,
有 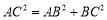
∴ 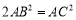
∴ 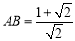 .
.
故正方形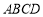 的边长为
的边长为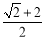
考点:1.切线的判定与性质;2.勾股定理;3.正方形的性质.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案科目:初中数学 来源:[同步]2015年课时同步练习(人教版)八年级数学下册18.1(解析版) 题型:解答题
(2013泸州)如图,已知□ABCD中,F是BC边的中点,连接DF并延长,交AB的延长线于点E.求证:AB=BE.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省滕州市九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图1,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).
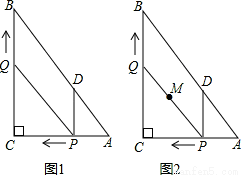
(1)直接用含t的代数式分别表示:QB= ,PD= .
(2)是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由.并探究如何改变Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度;
(3)如图2,在整个运动过程中,求出线段PQ中点M所经过的路径长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省滕州市九年级上学期期末考试数学试卷(解析版) 题型:选择题
若反比例函数 与二次函数
与二次函数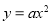 的图象的公共点在第三象限,则一次函数
的图象的公共点在第三象限,则一次函数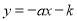 的图象不经过
的图象不经过
A.第一象限 B.第二象限 C.第三象限 D.第四象限
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省滕州市九年级上学期期末考试数学试卷(解析版) 题型:选择题
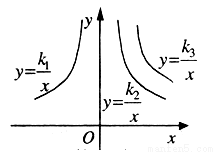
如下图是三个反比例函数 ,
,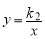 ,
,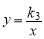 在
在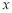 轴上方的图象,由此观察得到
轴上方的图象,由此观察得到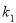 、
、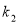 、
、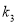 的大小关系为( )
的大小关系为( )
A.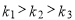 B.
B.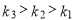 C.
C.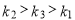 D.
D.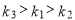
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省滕州市九年级上学期期末考试数学试卷(解析版) 题型:解答题
某射击运动员在相同条件下的射击160次,其成绩记录如下:
射击次数 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 |
射中9环以上的次数 | 15 | 33 | 63 | 79 | 97 | 111 | 130 | |
射中9环以上的频率 | 0.75 | 0.83 | 0.80 | 0.79 | 0.79 | 0.79 | 0.81 |
(1)根据上表中的信息将两个空格的数据补全(射中9环以上的次数为整数,频率精确到0.01);
(2)根据频率的稳定性,估计这名运动员射击一次时“射中9环以上”的概率(精确到0.1),并简述理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省兴化顾庄等三校九年级上学期期末考试数学试卷(解析版) 题型:解答题
(10分)如图,某居民小区有一朝向为正南方向的居民楼,该居民楼的一楼是高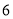 米的小区超市,超市以上是居民住房,在该楼的前面
米的小区超市,超市以上是居民住房,在该楼的前面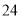 米处要盖一栋高
米处要盖一栋高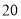 米的新楼.当冬季正午的阳光与水平线的夹角为
米的新楼.当冬季正午的阳光与水平线的夹角为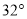 时.
时.
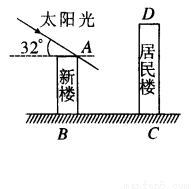
(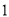 )问超市以上的居民住房采光是否有影响,为什么?
)问超市以上的居民住房采光是否有影响,为什么?
(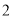 )若要使超市采光不受影响,两楼应相距多少米?
)若要使超市采光不受影响,两楼应相距多少米?
(参考数据:sin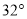 ≈
≈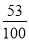 ,cos
,cos ≈
≈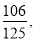
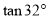 ≈
≈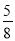 .)
.)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年重庆开县七年级上学期期末考试数学试卷(解析版) 题型:选择题
下列结论正确的是( )
A. 直线比射线长
B. 一条直线就是一个平角
C. 过三点中的任两点一定能作三条直线
D.经过两点有且只有一条直线
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com