
【题目】教材呈现:如图是华师版九年级上册数学教材第78页的部分内容.
例2 如图,在![]() 中,
中,![]() 分别是边
分别是边![]() 的中点,
的中点,![]() 相交于点
相交于点![]() ,求证:
,求证:![]() ,
,
证明:连结![]() .
.
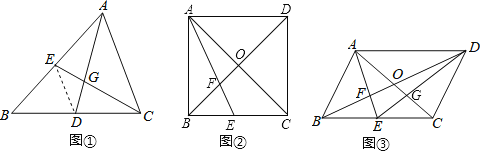
请根据教材提示,结合图①,写出完整的证明过程.
结论应用:在![]() 中,对角线
中,对角线![]() 交于点
交于点![]() ,
,![]() 为边
为边![]() 的中点,
的中点,![]() 、
、![]() 交于点
交于点![]() .
.
(1)如图②,若![]() 为正方形,且
为正方形,且![]() ,则
,则![]() 的长为 .
的长为 .
(2)如图③,连结![]() 交
交![]() 于点
于点![]() ,若四边形
,若四边形![]() 的面积为
的面积为![]() ,则
,则![]() 的面积为 .
的面积为 .
【答案】教材呈现:详见解析;结论应用:(1)![]() ;(2)6.
;(2)6.
【解析】
教材呈现:如图①,连结![]() .根据三角形中位线定理可得
.根据三角形中位线定理可得![]() ,
,![]() ,那么
,那么![]() ,由相似三角形对应边成比例以及比例的性质即可证明
,由相似三角形对应边成比例以及比例的性质即可证明![]() ;
;
结论应用:(1)如图②.先证明![]() ,得出
,得出![]() ,那么
,那么![]() ,又
,又![]() ,可得
,可得![]() ,由正方形的性质求出
,由正方形的性质求出![]() ,即可求出
,即可求出![]() ;
;
(2)如图③,连接![]() .由(1)易证
.由(1)易证![]() .根据同高的两个三角形面积之比等于底边之比得出
.根据同高的两个三角形面积之比等于底边之比得出![]() 与
与![]() 的面积比
的面积比![]() ,同理,
,同理,![]() 与
与![]() 的面积比=2,那么
的面积比=2,那么![]() 的面积
的面积![]() 的面积=2(
的面积=2(![]() 的面积
的面积![]() 的面积)=
的面积)=![]() ,所以
,所以![]() 的面积
的面积![]() ,进而求出
,进而求出![]() 的面积
的面积![]() .
.
教材呈现:
证明:

如图①,连结![]() .
.
∵在![]() 中,
中,![]() 分别是边
分别是边![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
结论应用:
(1)解:如图②.
∵四边形![]() 为正方形,
为正方形,![]() 为边
为边![]() 的中点,对角线
的中点,对角线![]() 、
、![]() 交于点
交于点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵正方形![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() .
.
故答案为![]() ;
;
(2)解:如图③,连接![]() .
.
由(1)知,![]() ,
,
∴![]() .
.
∵![]() 与
与![]() 的高相同,
的高相同,
∴![]() 与
与![]() 的面积比
的面积比![]() ,
,
同理,![]() 与
与![]() 的面积比=2,
的面积比=2,
∴![]() 的面积
的面积![]() 的面积=2(
的面积=2(![]() 的面积
的面积![]() 的面积)
的面积)![]() ,
,
∴![]() 的面积
的面积![]() ,
,
∴![]() 的面积
的面积![]() .
.
故答案为6.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
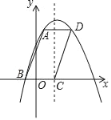
【题目】如图,ABCD与抛物线y=﹣x2+bx+c相交于点A,B,D,点C在抛物线的对称轴上,已知点B(﹣1,0),BC=4.
(1)求抛物线的解析式;
(2)求BD的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+3与x轴交于点A(﹣1,0),B(3,0).
(1)求抛物线的解析式;
(2)过点D(0,![]() )作x轴的平行线交抛物线于E,F两点,求EF的长;
)作x轴的平行线交抛物线于E,F两点,求EF的长;
(3)当y≤![]() 时,直接写出x的取值范围是 .
时,直接写出x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有甲,乙两种机器人都被用来搬运某体育馆室内装潢材料甲型机器人比乙型机器人每小时少搬运30千克,甲型机器人搬运600千克所用的时间与乙型机器人搬运800千克所用的时间相同,两种机器人每小时分别搬运多少千克?设甲型机器人每小时搬运x千克,根据题意,可列方程为( )
A. ![]() =
=![]() B.
B. ![]() =
=![]()
C. ![]() =
=![]() D.
D. ![]() =
=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形![]() 中,
中,![]() 是
是![]() 中点,点
中点,点![]() 从点
从点![]() 出发沿
出发沿![]() 的路线匀速运动,到点
的路线匀速运动,到点![]() 停止,点
停止,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 路线匀速运动,
路线匀速运动,![]() 、
、![]() 两点同时出发,点
两点同时出发,点![]() 的速度是点
的速度是点![]() 速度的
速度的![]() 倍
倍![]() ,当点
,当点![]() 停止时,点
停止时,点![]() 也同时停止运动,设
也同时停止运动,设![]() 秒时,正方形
秒时,正方形![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() ,
,![]() 关于
关于![]() 的函数关系如图2所示,则
的函数关系如图2所示,则
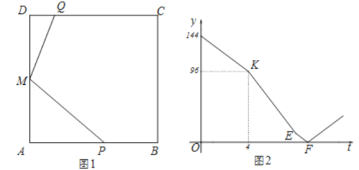
(1)求正方形边长![]() ;
;
(2)求![]() 的值;
的值;
(3)求图2中线段![]() 所在直线的解析式.
所在直线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
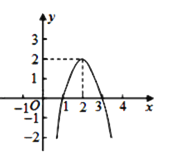
(1)写出方程ax2+bx+c=0的两个根;
(2)写出y随x的增大而减小的自变量x的取值范围;
(3)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
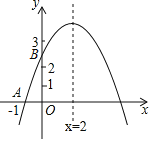
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,2)与(0,3)之间(不包括这两点),对称轴为直线x=2.下列结论:abc<0;②9a+3b+c>0;③若点M(![]() ,y1),点N(
,y1),点N(![]() ,y2)是函数图象上的两点,则y1<y2;④﹣
,y2)是函数图象上的两点,则y1<y2;④﹣![]() <a<﹣
<a<﹣![]() .其中正确结论有( )
.其中正确结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形 ACDE 是证明勾股定理时用到的一个图形,a 、b 、c 是 RtABC和 RtBED 的边长,已知![]() ,这时我们把关于 x 的形如
,这时我们把关于 x 的形如![]() 二次方程称为“勾系一元二次方程”.
二次方程称为“勾系一元二次方程”.

请解决下列问题:
(1)写出一个“勾系一元二次方程”;
(2)求证:关于 x 的“勾系一元二次方程”![]() ,必有实数根;
,必有实数根;
(3)若 x 1是“勾系一元二次方程” ![]() 的一个根,且四边形 ACDE 的周长是6
的一个根,且四边形 ACDE 的周长是6![]() ,求ABC 的面积.
,求ABC 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
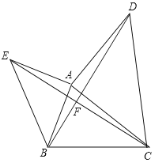
【题目】如图,已知△ABC,分别以AB,AC为直角边,向外作等腰直角三角形ABE和等腰直角三角形ACD,∠EAB=∠DAC=90°,连结BD,CE交于点F,设AB=m,BC=n.下列结论①∠BDA=∠ECA; ②若m=![]() ,n=3,∠ABC=75°,则BD=
,n=3,∠ABC=75°,则BD=![]() ;③当∠ABC=135°时,BD最大,最大值为
;③当∠ABC=135°时,BD最大,最大值为![]() m+n;④AE2=BF2+EF2中正确的有_______。
m+n;④AE2=BF2+EF2中正确的有_______。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com