
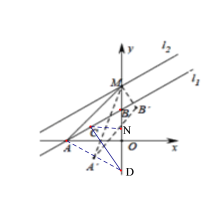
ЁОЬтФПЁПШчЭМЃЌжБЯпl1ЃКyЃНkx+bгыxжсЁЂyжсЗжБ№НЛгкAЃЌBСНЕуЃЌЦфжаЕуBЕФзјБъЮЊЃЈ0ЃЌ6ЃЉЃЌЁЯBAO=30ЁуНЋжБЯпl1бизХyжсе§ЗНЯђЦНвЦвЛЖЮОрРыЕУЕНжБЯпl2НЛyжсгкЕуMЃЌЧвl1гыl2жЎМфЕФОрРыЮЊ3ЃЌЕуCЃЈxЃЌyЃЉЪЧжБЯп11ЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуCзїABЕФДЙЯпCDНЛyжсгкЕуDЃЎ
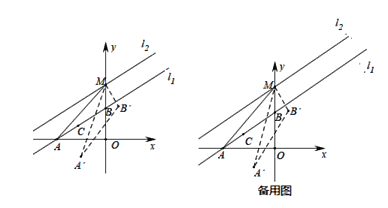
ЃЈ1ЃЉЧѓЕуMЕФзјБъКЭжБЯпl1ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕБCдЫЖЏЕНЪВУДЮЛжУЪБЃЌЁїAODЕФУцЛ§ЮЊ21![]() ЃЌЧѓГіДЫЪБЕуCЕФзјБъЃЛ
ЃЌЧѓГіДЫЪБЕуCЕФзјБъЃЛ
ЃЈ3ЃЉСЌНгAMЃЌНЋЁїABMШЦзХЕуMа§зЊЕУЕНЁїA'B'MЃЌдкЦНУцФкЪЧЗёДцдквЛЕуNЃЎЪЙЫФБпаЮAMA'NЮЊОиаЮЃПШєДцдкЃЌЧѓГіЕуNЕФзјБъЃКШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉM(0ЃЌ6+2![]() )ЃЌжБЯпl1ЕФНтЮіЪНЮЊЃКyЃН
)ЃЌжБЯпl1ЕФНтЮіЪНЮЊЃКyЃН![]() x+6ЃЛЃЈ2ЃЉЕуCЕФзјБъЮЊЃК(-
x+6ЃЛЃЈ2ЃЉЕуCЕФзјБъЮЊЃК(-![]() ЃЌ
ЃЌ![]() )Лђ(
)Лђ(![]() ЃЌ
ЃЌ![]() )ЃЛЃЈ3ЃЉЕуNЕФзјБъЮЊЃК(-6-8
)ЃЛЃЈ3ЃЉЕуNЕФзјБъЮЊЃК(-6-8![]() ЃЌ6
ЃЌ6![]() )Лђ(6-4
)Лђ(6-4![]() ЃЌ-6
ЃЌ-6![]() )ЃЎ
)ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЙ§ЕуBзїBHЁЭl1гкЕуHЃЌгЩl1ЁЮl2ЃЌЕУЁЯBMH=ЁЯOBA=60ЁуЃЌНјЖјЕУBM=2![]() ЃЌМДПЩЕУЕНMЕФзјБъЃЌгЩЬтвтЕУA(-6
ЃЌМДПЩЕУЕНMЕФзјБъЃЌгЩЬтвтЕУA(-6![]() ЃЌ0)ЃЌИљОнД§ЖЈЯЕЪ§ЗЈЃЌМДПЩЕУЕНД№АИЃЛ
ЃЌ0)ЃЌИљОнД§ЖЈЯЕЪ§ЗЈЃЌМДПЩЕУЕНД№АИЃЛ
ЃЈ2ЃЉСЌНгADЃЌЩшЕуD(0ЃЌm)ЃЌНсКЯЃЌЁїAODЕФУцЛ§ЮЊ21![]() ЃЌЧѓЕУmЕФжЕЮЊЁР7ЃЌЗжСНжжЧщПіЃКЂйЕБD(0ЃЌ-7)ЪБЃЌЂкЕБD(0ЃЌ7)ЪБЃЌЗжБ№ЧѓГіЕуCЕФзјБъМДПЩЃЛ
ЃЌЧѓЕУmЕФжЕЮЊЁР7ЃЌЗжСНжжЧщПіЃКЂйЕБD(0ЃЌ-7)ЪБЃЌЂкЕБD(0ЃЌ7)ЪБЃЌЗжБ№ЧѓГіЕуCЕФзјБъМДПЩЃЛ
ЃЈ3ЃЉгЩЫФБпаЮAMA'NЮЊОиаЮЃЌЧвMA = MA'ЃЌЕУЫФБпаЮAMA'NЮЊе§ЗНаЮЃЌЗжСНжжЧщПіЃКЂйЕБЕуNдкxжсЩЯЗНЪБЃЌЂкЕБЕуNдкxжсЯТЗНЪБЃЌЗжБ№ЧѓГіЕуNЕФзјБъМДПЩЃЎ
ЃЈ1ЃЉЁпЕуBЕФзјБъЮЊ(0ЃЌ6)ЃЌЁЯBAO=30ЁуЃЌЁЯAOB=90ЁуЃЌ
ЁрBO=6ЃЌAO=6![]() ЃЌ
ЃЌ
ЁрA(-6![]() ЃЌ0)ЃЌ
ЃЌ0)ЃЌ
Аб(0ЃЌ6)ЃЌ(-6![]() ЃЌ0)ЃЌДњШыyЃНkx+bЃЌЕУ
ЃЌ0)ЃЌДњШыyЃНkx+bЃЌЕУ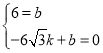 ЃЌНтЕУЃК
ЃЌНтЕУЃК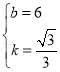 ЃЌ
ЃЌ
ЁржБЯпl1ЕФНтЮіЪНЮЊЃКyЃН![]() x+6ЃЌ
x+6ЃЌ
Й§ЕуBзїBHЁЭl1гкЕуHЃЌШчЭМ1ЃЌ
Ёпl1ЁЮl2ЃЌ
ЁрЁЯBMH=ЁЯOBA=90Ёу-30Ёу=60ЁуЃЌ
ЁрЁЯMBH=30ЁуЃЌ
ЁпBH=3ЃЌ
ЁрBM=3ЁТ![]() ЁС2=2
ЁС2=2![]() ЃЌ
ЃЌ
ЁрM(0ЃЌ6+2![]() )ЃЛ
)ЃЛ
ЃЈ2ЃЉСЌНгADЃЌЩшЕуD(0ЃЌm)ЃЌ
гЩЬтвтЕУЃК![]() OAOD=21
OAOD=21![]() ЃЌ
ЃЌ
Ёр![]() ЁС6
ЁС6![]() ЁС
ЁС![]() =21
=21![]() ЃЌНтЕУЃКm=ЁР7ЃЌ
ЃЌНтЕУЃКm=ЁР7ЃЌ
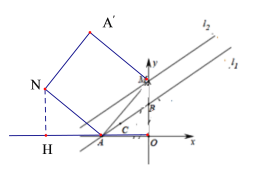
ЂйЕБD(0ЃЌ-7)ЪБЃЌЙ§ЕуCзїCNЁЭyжсгкЕуNЃЌШчЭМ2ЃЌ
ЁпCDЁЭl2ЃЌ
ЁрЁЯCDB=90Ёу-ЁЯABO=90Ёу-60Ёу=30ЁуЃЌ
ЁпBD=OB+OD=6+7=13ЃЌ
ЁрCD=13ЁТ2ЁС![]() =
=![]() ЃЌCN=
ЃЌCN=![]() CD=
CD=![]() ЃЌDN=
ЃЌDN=![]() CN=
CN=![]() ЃЌ
ЃЌ
ЁрON=![]() -7=
-7=![]() ЃЌ
ЃЌ
ЁрC(-![]() ЃЌ
ЃЌ![]() )ЃЛ
)ЃЛ
ЂкЕБD(0ЃЌ7)ЪБЃЌЭЌРэПЩЕУЃКC(![]() ЃЌ
ЃЌ![]() )ЃЌ
)ЃЌ
злЩЯЫљЪіЃКЕуCЕФзјБъЮЊЃК(-![]() ЃЌ
ЃЌ![]() )Лђ(
)Лђ(![]() ЃЌ
ЃЌ![]() )ЃЛ
)ЃЛ
ЃЈ3ЃЉДцдкЃЌРэгЩШчЯТЃК
ЁпЫФБпаЮAMA'NЮЊОиаЮЃЌЧвMA = MA'ЃЌ
ЁрЫФБпаЮAMA'NЮЊе§ЗНаЮЃЌ
ЁрAN=AMЃЌ
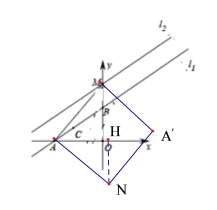
ЂйЕБЕуNдкxжсЩЯЗНЪБЃЌЙ§ЕуNзїNHЁЭxжсгкЕуNЃЌШчЭМ3ЃЌ
ЁпЁЯAHN=ЁЯMAN=ЁЯAOM=90ЁуЃЌ
ЁрЁЯHAN+ЁЯOAM=ЁЯOAM+ЁЯAMO=90ЁуЃЌ
ЁрЁЯHAN=ЁЯAMOЃЌ
ЁрAHNMOAЃЈAASЃЉЃЌ
ЁрNH=OA=6![]() ЃЌAH=OM=6+2
ЃЌAH=OM=6+2![]() ЃЌ
ЃЌ
ЁрOH=AH+OA=6+8![]() ЃЌ
ЃЌ
ЁрN(-6-8![]() ЃЌ6
ЃЌ6![]() )ЃЌ
)ЃЌ
ЂкЕБЕуNдкxжсЯТЗНЪБЃЌЙ§ЕуNзїNHЁЭxжсгкЕуNЃЌШчЭМ4ЃЌ
ЭЌРэПЩЕУЃКAHNMOAЃЈAASЃЉЃЌ
ЁрNH=OA=6![]() ЃЌAH=OM=6+2
ЃЌAH=OM=6+2![]() ЃЌ
ЃЌ
ЁрOH=AH-OA=6-4![]() ЃЌ
ЃЌ
ЁрN(6-4![]() ЃЌ-6
ЃЌ-6![]() )ЃЌ
)ЃЌ
злЩЯЫљЪіЃКЕуNЕФзјБъЮЊЃК(-6-8![]() ЃЌ6
ЃЌ6![]() )Лђ(6-4
)Лђ(6-4![]() ЃЌ-6
ЃЌ-6![]() )ЃЎ
)ЃЎ
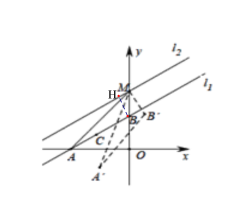
ЭМ1 ЭМ2
ЭМ3 ЭМ4


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
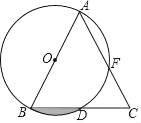
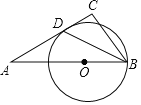
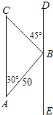
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌBDЪЧЁбOЕФЯвЃЌбгГЄBDЕНЕуCЃЌЪЙDC=BDЃЌСЌНсACНЛЁбOгкЕуFЃЎ
ЃЈ1ЃЉABгыACЕФДѓаЁгаЪВУДЙиЯЕЃПЧыЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШєAB=8ЃЌЁЯBAC=45ЁуЃЌЧѓЃКЭМжавѕгАВПЗжЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌЁЯA=30ЁуЃЌЕуOЪЧБпABЩЯвЛЕуЃЌвдЕуOЮЊдВаФЃЌвдOBЮЊАыОЖзїдВЃЌЁбOЧЁКУгыACЯрЧагкЕуDЃЌСЌНгBDЃЎШєBDЦНЗжЁЯABCЃЌAD=2![]() ЃЌдђЯпЖЮCDЕФГЄЪЧЃЈЁЁЁЁЃЉ
ЃЌдђЯпЖЮCDЕФГЄЪЧЃЈЁЁЁЁЃЉ
A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
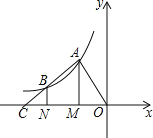
ЁОЬтФПЁПШчЭМЃЌЕуAЁЂBдкЗДБШР§КЏЪ§y=![]() ЕФЭМЯѓЩЯЃЌЙ§ЕуAЁЂBзїxжсЕФДЙЯпЃЌДЙзуЗжБ№ЪЧMЁЂNЃЌЩфЯпABНЛxжсгкЕуCЃЌШєOM=MN=NCЃЌЫФБпаЮAMNBЕФУцЛ§ЪЧ3ЃЌдђkЕФжЕЮЊЃЈ ЃЉ
ЕФЭМЯѓЩЯЃЌЙ§ЕуAЁЂBзїxжсЕФДЙЯпЃЌДЙзуЗжБ№ЪЧMЁЂNЃЌЩфЯпABНЛxжсгкЕуCЃЌШєOM=MN=NCЃЌЫФБпаЮAMNBЕФУцЛ§ЪЧ3ЃЌдђkЕФжЕЮЊЃЈ ЃЉ
AЃЎ2 BЃЎ4 CЃЎЉ2 DЃЎЉ4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
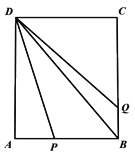
ЁОЬтФПЁПдкОиаЮABCDжаЃЌAB=2cmЃЌBC=3cmЃЌЕуPбиBЁњAЁњDдЫЖЏЃЌдЫЖЏЕНЕуDЪБЭЃжЙдЫЖЏЃЌЕуPдЫЖЏЕФЭЌЪБЃЌСэвЛЕуQДгBЁњCдЫЖЏЃЌЫйЖШЪЧЕуPЕФвЛАыЃЌЕБЕуPЭЃжЙдЫЖЏЪБЃЌЕуQвВЭЃжЙдЫЖЏЃЎЩшЕуPдЫЖЏЕФТЗГЬЮЊxcmЃЌЦфжаЩш![]() ,ПЩПЩИљОнбЇЯАКЏЪ§ЕФОбщЃЌЖдКЏЪ§yЫцздБфСПxЕФБфЛЏЖјБфЛЏЕФЙцТЩНјааСЫЬНОПЃЌЯТУцЪЧПЩПЩЕФЬНОПЙ§ГЬЃЌЧыВЙГфЭъећЃЎ
,ПЩПЩИљОнбЇЯАКЏЪ§ЕФОбщЃЌЖдКЏЪ§yЫцздБфСПxЕФБфЛЏЖјБфЛЏЕФЙцТЩНјааСЫЬНОПЃЌЯТУцЪЧПЩПЩЕФЬНОПЙ§ГЬЃЌЧыВЙГфЭъећЃЎ
ЃЈ1ЃЉШчЭМЪЧЛГіЕФКЏЪ§![]() гыxЕФКЏЪ§ЭМЯѓЃЌЙлВьЭМЯѓЃЎЕБx=1ЪБЃЌ
гыxЕФКЏЪ§ЭМЯѓЃЌЙлВьЭМЯѓЃЎЕБx=1ЪБЃЌ![]() =_____ЃЛВЂаДГіКЏЪ§ЕФвЛЬѕаджЪЃК________________________________________ЃЎ
=_____ЃЛВЂаДГіКЏЪ§ЕФвЛЬѕаджЪЃК________________________________________ЃЎ
ЃЈ2ЃЉЧыАяжњПЩПЩаДГі![]() гыxЕФКЏЪ§ЙиЯЕЪНЃЈВЛгУаДГіШЁжЕЗЖЮЇЃЉ__________________ЃЎ
гыxЕФКЏЪ§ЙиЯЕЪНЃЈВЛгУаДГіШЁжЕЗЖЮЇЃЉ__________________ЃЎ
ЃЈ3ЃЉЧыАДееСаБэЁЂУшЕуЁЂСЌЯпЕФВНжшдкЭЌвЛжБНЧзјБъЯЕжаЃЌЛГіКЏЪ§![]() ЕФЭМЯѓЃЎ
ЕФЭМЯѓЃЎ
ЃЈ4ЃЉНсКЯЛГіКЏЪ§ЭМЯѓЃЌНтОіЮЪЬтЃКЕБ![]() ЪБЃЌЕуPдЫЖЏЕФТЗГЬx=_______ЃЎ
ЪБЃЌЕуPдЫЖЏЕФТЗГЬx=_______ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
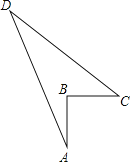
ЁОЬтФПЁПШчЭМЃЌвЛПщаЮШчЫФБпаЮABCDЕФВнЕижаЃЌABЃН3mЃЌBCЃН4mЃЌCDЃН12mЃЌDAЃН13mЃЌЧвЁЯABCЃН90ЁуЃЌвЊвдACЁЂCDЁЂDAЮЊБпжЦзїЮЇРИЃЌЮЪЮЇРИГЄЖрЩйУзЃЌВнЕиУцЛ§ЖрДѓЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛМмЭтЙњеьВьЛњби![]() ЗНЯђЧжШыЮвЙњСьПеНјааЗЧЗЈеьВьЃЌЮвПеОќЕФеНЖЗЛњби
ЗНЯђЧжШыЮвЙњСьПеНјааЗЧЗЈеьВьЃЌЮвПеОќЕФеНЖЗЛњби![]() ЗНЯђгыЭтЙњеьВьЛњЦНааЗЩааЃЌНјааИњзйМрЪгЃЌЮвЛњдк
ЗНЯђгыЭтЙњеьВьЛњЦНааЗЩааЃЌНјааИњзйМрЪгЃЌЮвЛњдк![]() ДІгыЭтЙњеьВьЛњ
ДІгыЭтЙњеьВьЛњ![]() ДІЕФОрРыЮЊ
ДІЕФОрРыЮЊ![]() УзЃЌ
УзЃЌ![]() ЮЊ
ЮЊ![]() ЃЌетЪБЭтЙњеьВьЛњЭЛШЛзЊЯђЃЌвдЦЋзѓ
ЃЌетЪБЭтЙњеьВьЛњЭЛШЛзЊЯђЃЌвдЦЋзѓ![]() ЕФЗНЯђЗЩааЃЌЮвЛњМЬајби
ЕФЗНЯђЗЩааЃЌЮвЛњМЬајби![]() ЗНЯђвд
ЗНЯђвд![]() Уз/УыЕФЫйЖШЗЩааЃЌЭтЙњеьВьЛњдк
Уз/УыЕФЫйЖШЗЩааЃЌЭтЙњеьВьЛњдк![]() ЕуЙЪвтзВЛїЮвеНЖЗЛњЃЌЪЙЮвеНЖЗЛњЪмЫ№ЃЎЮЪЭтЙњеьВьЛњгЩ
ЕуЙЪвтзВЛїЮвеНЖЗЛњЃЌЪЙЮвеНЖЗЛњЪмЫ№ЃЎЮЪЭтЙњеьВьЛњгЩ![]() ЕН
ЕН![]() ЕФЫйЖШЪЧЖрЩйЃПЃЈНсЙћБЃСєећЪ§ЃЌВЮПМЪ§Он
ЕФЫйЖШЪЧЖрЩйЃПЃЈНсЙћБЃСєећЪ§ЃЌВЮПМЪ§Он![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ2017еуНЪЁКўжнЪаЃЌЕк23ЬтЃЌ10ЗжЃЉКўжнЫигагуУзжЎЯчжЎГЦЃЌФГЫЎВњбјжГДѓЛЇЮЊСЫИќКУЕиЗЂЛгММЪѕгХЪЦЃЌвЛДЮадЪеЙКСЫ20000kgЕЫЎгуЃЌМЦЛЎбјжГвЛЖЮЪБМфКѓдйГіЪлЃЎвбжЊУПЬьЗХбјЕФЗбгУЯрЭЌЃЌЗХбј10ЬьЕФзмГЩБОЮЊ30.4ЭђдЊЃЛЗХбј20ЬьЕФзмГЩБОЮЊ30.8ЭђдЊЃЈзмГЩБО=ЗХбјзмЗбгУ+ЪеЙКГЩБОЃЉЃЎ
ЃЈ1ЃЉЩшУПЬьЕФЗХбјЗбгУЪЧaЭђдЊЃЌЪеЙКГЩБОЮЊbЭђдЊЃЌЧѓaКЭbЕФжЕЃЛ
ЃЈ2ЃЉЩшетХњЕЫЎгуЗХбјtЬьКѓЕФжЪСПЮЊmЃЈkgЃЉЃЌЯњЪлЕЅМлЮЊyдЊ/kgЃЎИљОнвдЭљОбщПЩжЊЃКmгыtЕФКЏЪ§ЙиЯЕЮЊ![]() ЃЛyгыtЕФКЏЪ§ЙиЯЕШчЭМЫљЪОЃЎ
ЃЛyгыtЕФКЏЪ§ЙиЯЕШчЭМЫљЪОЃЎ
ЂйЗжБ№ЧѓГіЕБ0ЁмtЁм50КЭ50ЃМtЁм100ЪБЃЌyгыtЕФКЏЪ§ЙиЯЕЪНЃЛ
ЂкЩшНЋетХњЕЫЎгуЗХбјtЬьКѓвЛДЮадГіЪлЫљЕУРћШѓЮЊWдЊЃЌЧѓЕБtЮЊКЮжЕЪБЃЌWзюДѓЃПВЂЧѓГізюДѓжЕЃЎЃЈРћШѓ=ЯњЪлзмЖюЉзмГЩБОЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
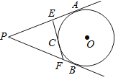
ЁОЬтФПЁПШчЭМЃЌ![]() ЁЂ
ЁЂ![]() ЗжБ№Ча
ЗжБ№Ча![]() гк
гк![]() ЁЂ
ЁЂ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЪЧСгЛЁ
ЪЧСгЛЁ![]() ЩЯЕФЕуЃЈВЛгыЕу
ЩЯЕФЕуЃЈВЛгыЕу![]() ЁЂ
ЁЂ![]() жиКЯЃЉЃЌЙ§Еу
жиКЯЃЉЃЌЙ§Еу![]() ЕФЧаЯпЗжБ№НЛ
ЕФЧаЯпЗжБ№НЛ![]() ЁЂ
ЁЂ![]() гкЕу
гкЕу![]() ЁЂ
ЁЂ![]() ЃЎдђ
ЃЎдђ![]() ЕФжмГЄЮЊЃЈ ЃЉ
ЕФжмГЄЮЊЃЈ ЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com