Question

若一个四边形的一条对角线把四边形分成两个等腰三角形，我们把这条对角线叫这个四边形的和谐线，这个四边形叫做和谐四边形．如菱形就是和谐四边形．

（1）如图1，在梯形ABCD中，AD∥BC，∠BAD=120°，∠C=75°，BD平分∠ABC．求证：BD是梯形ABCD的和谐线；

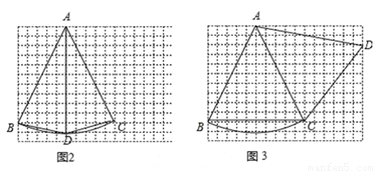
（2）如图2，在12×16的网格图上（每个小正方形的边长为1）有一个扇形BAC，点A．B．C均在格点上，请在答题卷给出的两个网格图上各找一个点D，使得以A、B、C、D为顶点的四边形的两条对角线都是和谐线，并画出相应的和谐四边形；

（3）四边形ABCD中，AB=AD=BC，∠BAD=90°，AC是四边形ABCD的和谐线，求∠BCD的度数．

 

Answer 1

【答案】

解：（1）∵AD∥BC，∴∠ABC+∠BAD=180°，∠ADB=∠DBC。

∵∠BAD=120°，∴∠ABC=60°。

∵BD平分∠ABC，∴∠ABD=∠DBC=30°。

∴∠ABD=∠ADB。∴△ADB是等腰三角形。

在△BCD中，∠C=75°，∠DBC=30°，∴∠BDC=∠C=75°。∴△BCD为等腰三角形。

∴BD是梯形ABCD的和谐线。

（2）由题意作图为：图2，图3

 

（3）∵AC是四边形ABCD的和谐线，∴△ACD是等腰三角形。

∵AB=AD=BC，∴分三种情况：

如图4，当AD=AC时，

图4

∴AB=AC=BC，∠ACD=∠ADC。

∴△ABC是正三角形。∴∠BAC=∠BCA=60°。

∵∠BAD=90°，∴∠CAD=30°。

∴∠ACD=∠ADC=75°。∴∠BCD=60°+75°=135°。

如图5，当AD=CD时，

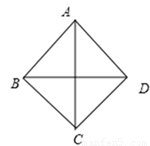
图5

∴AB=AD=BC=CD。

∵∠BAD=90°，∴四边形ABCD是正方形。

∴∠BCD=90°。

如图6，当AC=CD时，

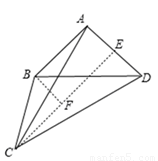
图6

过点C作CE⊥AD于E，过点B作BF⊥CE于F，

∵AC=CD．CE⊥AD，∴AE=AD，∠ACE=∠DCE。

∵∠BAD=∠AEF=∠BFE=90°，

∴四边形ABFE是矩形。∴BF=AE。

∵AB=AD=BC，∴BF=BC。∴∠BCF=30°。

∵AB=BC，∴∠ACB=∠BAC。

∵AB∥CE，∴∠BAC=∠ACE。∴∠ACB=∠ACE=∠BCF=15°。

∴∠BCD=15°×3=45°。

综上所述，∠BCD的度数为135°或90°或45°。

【解析】（1）要证明BD是四边形ABCD的和谐线，只需要证明△ABD和△BDC是等腰三角形即可。

（2）根据扇形的性质弧上的点到顶点的距离相等，只要D在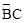上任意一点构成的四边形ABDC就是和谐四边形；连接BC，在△BAC外作一个以AC为腰的等腰三角形ACD，构成的四边形ABCD就是和谐四边形。

（3）由AC是四边形ABCD的和谐线，可以得出△ACD是等腰三角形，从图4，图5，图6三种情况运用等边三角形的性质，正方形的性质和30°的直角三角形性质就可以求出∠BCD的度数。