
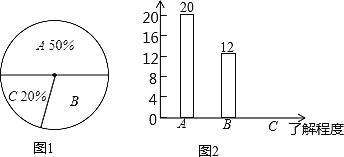
����Ŀ��˫���ؽ�����Ҫ���ѧУ��ǿ��ѧ���İ�ȫ����,ȫ�ظ���СѧУ����߶�����,С�վͱ���ͬѧ��ȫ֪ʶ���˽�̶Ƚ�����һ�ε���ͳ��.����ͳ�ƽ����Ϊ����,A:��Ϥ��B:�˽�϶ࣻC:һ���˽⡣ͼ����ͼ�������ɼ����ݺ�,���Ƶ�������������ͳ��ͼ,�������ͼ���ṩ����Ϣ�����������:
(1)��С�����ڵİ༶���ж�����ѧ����
(2)������ͼ��,����ʾ��һ���˽⡱�IJ��ֲ�����������
(3)������ͳ��ͼ��,���㡰�˽�϶ࡱ��������Ӧ������Բ�ĽǵĶ�����
(4)���С�������꼶��1000��ͬѧ,�������ȫ�꼶��ȫ֪ʶ���˽�϶ࡱ��ѧ������.
���𰸡���1��40�ˣ���2��ͼ�μ���������3��108�㣻��4����Լ��300��.
��������
��1������A��ռ�İٷֱȺ���Ӧ��Ƶ�����������
��2������C��ռ�İٷֱȺ����������C��Ƶ�����ɣ�
��3��������˽�϶���������ռ�ı���������������˽�϶�����������Ӧ��Բ�ĽǵĶ�����
��4�����������������壬�������ȫ�꼶��ȫ֪ʶ���˽�϶�����ѧ����Լ��1000����1-50%-20%��=300�ˣ�
�⣺��1����20��50%=40���ˣ���
�𣺸ð��40��ѧ����
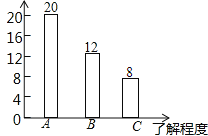
��2��C��һ���˽������Ϊ��40��20%=8���ˣ�������ͼ��ͼ��ʾ��
 ��
��
��3��360�����1-50%-20%��=108��������������ͳ��ͼ�У����˽�϶�����������Ӧ��Բ�ĽǵĶ���Ϊ108����
��4��1000����1-50%-20%��=300������ȫ�꼶��ȫ֪ʶ���˽�϶�����ѧ����Լ��300�ˣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
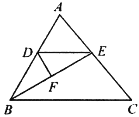
����Ŀ����ͼ���ڡ�ABC �У�BE ƽ�֡�ABC��DE��BC.
��1���жϡ�DBE ��ʲô�����Σ���˵�����ɣ�
��2���� F Ϊ BE �е㣬��ABC��58�㣬��˵�� DF��BE�������EDF �Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Ӫ��ij��ѧУ��ί��չ���ذ��м���ͯ�����ľ�����ȫУʦ��ӻԾ���������鼮��3000��.Ϊ���˽�����鼮�ķֲ���������������ȡ�˲����鼮���������ͳ�ƣ�A.�����ࣻB.��ѧ�ࣻC.�����ࣻD.����������ͳ�ƽ�����Ƴ���ͼ��ʾ��������������ͳ��ͼ.

��1�����ͳ�ƹ���ȡ_____���鼮������ͳ��ͼ�е�m=______���Ϧ��Ķ�����_____
��2���뽫����ͳ��ͼ����������
��3������ȫУʦ���������˶��ٱ���ѧ���鼮.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90������A��ƽ���߽�BC��D. ��C����CG��AB��G����AD��E. ��D����DF��AB��F. ���н��ۣ��١�CED=��CDE����S��AEC��S��AEG=AC��AG���ۡ�ADF=2��FDB����CE=DF.������ȷ�Ľ����У� ��
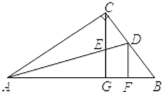
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���̳�����һ�ֵ���Ϊ40Ԫ�����������Ե���50Ԫ���ۣ���ôÿ�¿��۳�30�����������۾��飬�ۼ�ÿ���5Ԫ����������Ӧ����1��.
��1����д�����۵������![]() Ԫ���ܵ���������yԪ֮��ĺ�����ϵʽ��
Ԫ���ܵ���������yԪ֮��ĺ�����ϵʽ��
��2��������Ǿ�����Ϊʹÿ�µ��������������ô��ȷ����������ĵ���Ϊ����Ԫ����ʱ����������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����κ���y=ax2+bx+c��x��Ľ���Ϊ��x1��0������x2��0������x1��x2��������ax2+bx+c��a=0������Ϊm��n��m��n����������˵����ȷ������������
A. x1+x2��m+n B. m��n��x1��x2 C. x1��m��n��x2 D. m��x1��x2��n
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������㣺![]() .
.
���磺3![]() 2=3��3-2��=3��-1
2=3��3-2��=3��-1![]() 4=-1
4=-1![]() ��-1-4��=5.
��-1-4��=5.
��1����ֱ��д��3![]() a=b�������������⣻
a=b�������������⣻
��2����֪2![]() a=5b-2m��3
a=5b-2m��3![]() b=5a+m��˵����12a+11b��ֵ��m�أ�
b=5a+m��˵����12a+11b��ֵ��m�أ�
��3����֪a>1,��M=ab![]() b��N=b
b��N=b![]() ab���ԱȽ�M,N�Ĵ�С.
ab���ԱȽ�M,N�Ĵ�С.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������꼶Ϊ���˽�ѧ����ѧ�Ľ�ͨ��ʽ���ִӳ����꼶ѧ���������ȡ�˲���ѧ������������ѧ�Ľ�ͨ��ʽ���ʾ����ˣ��涨ÿ�˱��벢��ֻ���ڡ��˳����������С������ﳵ���͡�������������ѡ��һ�����ͳ�ƽ������������������������ͳ��ͼ��

�����������⣺
��1������ε����У�һ������������ ��ѧ����
��2������ͳ��ͼ���ﳵ�������ε�Բ�ĽǵĶ���Ϊ ����
��3����ȫ����ͳ��ͼ��
��4���������꼶����1500��ѧ�����Թ��Ƴ����꼶ѧ����ѡ���С���ʽ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB��AC����ABΪֱ���ġ�O�ֱ���BC��AC���ڵ�D��E������D��DF��AC�ڵ�F.
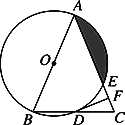
(1)�ж�DF���ǡ�O��λ�ù�ϵ����֤����Ľ��ۡ�
(2)����O�İ뾶Ϊ4����CDF��22.5��������Ӱ���ֵ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com