
【题目】一艘轮船位于灯塔P南偏西60°方向,距离灯塔20海里的A处,它向东航行多少海里到达灯塔P南偏西45°方向上的B处(参考数据:![]() ≈1.732,结果精确到0.1)?
≈1.732,结果精确到0.1)?
【答案】它向东航行约7.3海里到达灯塔P南偏西45°方向上的B处.
【解析】
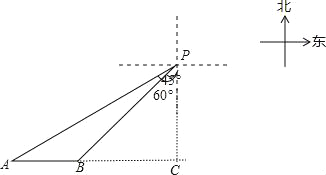
利用题意得到AC⊥PC,∠APC=60°,∠BPC=45°,AP=20,如图,在Rt△APC中,利用余弦的定义计算出PC=10,利用勾股定理求出AC,再判断△PBC为等腰直角三角形得到BC=PC=10,然后计算AC-BC即可.
如图,AC⊥PC,∠APC=60°,∠BPC=45°,AP=20,
在Rt△APC中,∵cos∠APC=![]() ,
,
∴PC=20cos60°=10,
∴AC=![]() =10
=10![]() ,
,
在△PBC中,∵∠BPC=45°,
∴△PBC为等腰直角三角形,
∴BC=PC=10,
∴AB=AC﹣BC=10![]() ﹣10≈7.3(海里),
﹣10≈7.3(海里),
答:它向东航行约7.3海里到达灯塔P南偏西45°方向上的B处.


科目:初中数学 来源: 题型:
【题目】“驴友”小明分三次从M地出发沿着不同的线路![]() 线,B线,C线
线,B线,C线![]() 去N地
去N地![]() 在每条线路上行进的方式都分为穿越丛林、涉水行走和攀登这三种
在每条线路上行进的方式都分为穿越丛林、涉水行走和攀登这三种![]() 他涉水行走4小时的路程与攀登6小时的路程相等
他涉水行走4小时的路程与攀登6小时的路程相等![]() 线、C线路程相等,都比A线路程多
线、C线路程相等,都比A线路程多![]() ,A线总时间等于C线总时间的
,A线总时间等于C线总时间的![]() ,他用了3小时穿越丛林、2小时涉水行走和2小时攀登走完A线,在B线中穿越丛林、涉水行走和攀登所用时间分别比A线上升了
,他用了3小时穿越丛林、2小时涉水行走和2小时攀登走完A线,在B线中穿越丛林、涉水行走和攀登所用时间分别比A线上升了![]() ,
,![]() ,
,![]() ,若他用了x小时穿越丛林、y小时涉水行走和z小时攀登走完C线,且x,y,z都为正整数,则
,若他用了x小时穿越丛林、y小时涉水行走和z小时攀登走完C线,且x,y,z都为正整数,则![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
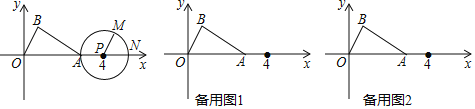
【题目】已知:如图,在Rt△ABO中,∠B=90°,∠OAB=30°,OA=3.以点O为原点,斜边OA所在直线为x轴,建立平面直角坐标系,以点P(4,0)为圆心,PA长为半径画圆,⊙P与x轴的另一交点为N,点M在⊙P上,且满足∠MPN=60°.⊙P以每秒1个单位长度的速度沿x轴向左运动,设运动时间为ts,解答下列问题:
(发现)(1)![]() 的长度为多少;
的长度为多少;
(2)当t=2s时,求扇形MPN(阴影部分)与Rt△ABO重叠部分的面积.
(探究)当⊙P和△ABO的边所在的直线相切时,求点P的坐标.
(拓展)当![]() 与Rt△ABO的边有两个交点时,请你直接写出t的取值范围.
与Rt△ABO的边有两个交点时,请你直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
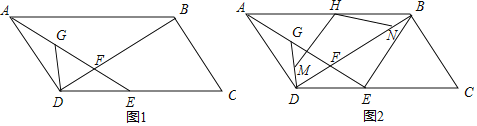
【题目】如图,在平行四边形ABCD中,对角线BD⊥AD,E为CD上一点,连接AE交BD于点F,G为AF的中点,连接DG.
(1)如图1,若DG=DF=1,BF=3,求CD的长;
(2)如图2,连接BE,且BE=AD,∠AEB=90°,M、N分别为DG,BD上的点,且DM=BN,H为AB的中点,连接HM、HN,求证:∠MHN=∠AFB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.掷一枚均匀的骰子,骰子停止转动后,6点朝上是必然事件
B.甲、乙两人在相同条件下各射击10次,他们的成绩平均数相同,方差分别是![]() ,
,![]() ,则甲的射击成绩较稳定
,则甲的射击成绩较稳定
C.“明天降雨的概率为![]() ”,表示明天有半天都在降雨
”,表示明天有半天都在降雨
D.了解一批电视机的使用寿命,适合用普查的方式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校体育组为了解全校学生“最喜欢的一项球类项目”,随机抽取了部分学生进行调查,下面是根据调查结果绘制的不完整的统计图:
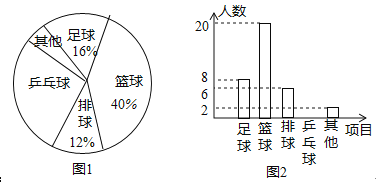
请你根据统计图回答下列问题:
(1)喜欢乒乓球的学生所占的百分比是多少?并请补全条形统计图;
(2)请你估计全校500名学生中最喜欢“排球”项目的有多少名?
(3)在扇形统计图中,“篮球”部分所对应的圆心角是多少度?
(4)篮球教练在制定训练计划前,将从最喜欢篮球项目的甲、乙、丙、丁四名同学中任选两人进行个别座谈,请用列表法或树状图法求抽取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
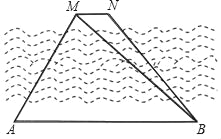
【题目】如图,在一条河的北岸有两个目标M、N,现在位于它的对岸设定两个观测点A、B.已知AB∥MN,在A点测得∠MAB=60°,在B点测得∠MBA=45°,AB=600米.
(1)求点M到AB的距离;(结果保留根号)
(2)在B点又测得∠NBA=53°,求MN的长.(结果精确到1米)
(参考数据:![]() ≈1.732,sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75)
≈1.732,sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
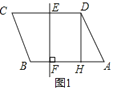
【题目】如图1,在ABCD中,DH⊥AB于点H,CD的垂直平分线交CD于点E,交AB于点F,AB=6,DH=4,BF:FA=1:5.
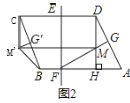
(1)如图2,作FG⊥AD于点G,交DH于点M,将△DGM沿DC方向平移,得到△CG′M′,连接M′B.
①求四边形BHMM′的面积;
②直线EF上有一动点N,求△DNM周长的最小值.
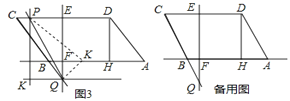
(2)如图3,延长CB交EF于点Q,过点Q作QK∥AB,过CD边上的动点P作PK∥EF,并与QK交于点K,将△PKQ沿直线PQ翻折,使点K的对应点K′恰好落在直线AB上,求线段CP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com