
 如图,长方形ABCD的长为a,宽为b,分别以A,B为圆心,以AD,BC为半径作两个圆.
如图,长方形ABCD的长为a,宽为b,分别以A,B为圆心,以AD,BC为半径作两个圆.分析 (1)根据图形可得阴影部分的周长是$\frac{1}{2}$×2πb+a+(a-2b);阴影部分的面积为长方形的面积减去两个$\frac{1}{4}$圆的面积(半圆的面积)即可;
(2)将a、b的值代入(1)中所列代数式求值即可.
解答 解:(1)阴影部分的周长L=$\frac{1}{2}$×2πb+a+(a-2b)=πb+2a-2b;
阴影部分的面积S=ab-$\frac{1}{2}$πb2;
(2)当a=8,b=3时,L=3π+16-6=10+3π,
S=8×3-$\frac{1}{2}$π×9=24-$\frac{9}{2}$π.
点评 此题考查的是列代数式和代数式求值,用到的知识点是半圆的周长和面积的计算方法.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
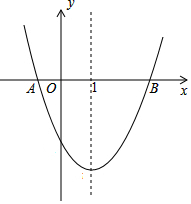 如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于A、B两点、点A在点B的左侧,它的顶点D(1,-4).
如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于A、B两点、点A在点B的左侧,它的顶点D(1,-4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
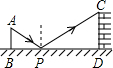 如图是小明测量某古城墙高度的示意图,点P处放一水平的平面镜,然后,后退至点B,从点A经平面镜刚好看到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是( )
如图是小明测量某古城墙高度的示意图,点P处放一水平的平面镜,然后,后退至点B,从点A经平面镜刚好看到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是( )| A. | 6米 | B. | 8米 | C. | 18米 | D. | 24米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com