
如图,已知△ABC,分别以AB、AC为边作△ABD和△ACE,且AD=AB,AC=AE,∠DAB=∠CAE,连接DC与BE.G、F分别是DC与BE的中点.
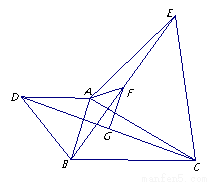
(1)求证:DC=BE;
(2)当∠DAB=80°,求∠AFG的度数;
(3)若∠DAB=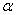 ,则∠AFG与
,则∠AFG与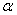 的数量关系是 .
的数量关系是 .
(1)证明见解析;(2)50°;(3)∠AFG= 90°-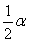 .
.
【解析】
试题分析:(1)由∠DAB=∠CAE知∠DAC=∠BAE,又DA=AB,AE=AC,所以△ADC≌△ABE,由此可得:DC=BE;
(2)易证△ADC≌△ABE可得CG=EF;又AE=AC,∠AEF=∠ACG,EF=CG,所以△AEF≌△AGC.可得AF=AG,且∠EAF=∠CAG,所以∠AFG=∠AGF,∠FAG=∠EAC=80°从而可求∠AFG=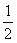 (180°-80°)=50°.
(180°-80°)=50°.
(3)由(2)知:∠AFG=90°-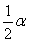 .
.
试题解析:(1)∵∠DAB=∠CAE∠D
∴AC=∠BAE,
又DA=AB,AE=AC,
所以△ADC≌△ABE
∴DC=BE;
(2)当∠DAB=80°.∵∠DAB=∠CAE,
∴∠DAB+∠BAC=∠CAE+∠CAE,
即∠DAC=∠BAE,
在△ADC与△ABE中,

∴△ADC≌△ABE ,
∴DC=BE,∠AEF=∠ACG,
∵G、F分别是DC与BE的中点,
∴CG=EF;
连AG,在△AEF与△AGC中,
∵AE=AC,∠AEF=∠ACG,EF=CG
∴△AEF≌△AGC,
∴AF=AG,且∠EAF=∠CAG,
∴∠AFG=∠AGF,∠FAG=∠EAC=80°,
∴∠AFG=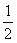 (180°-80°)=50°.
(180°-80°)=50°.
(3)∠AFG=90°-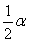 .
.
考点: 全等三角形的判定与性质.


科目:初中数学 来源:2015届江苏扬州宝应中南片七所学校初二12月月考数学卷(解析版) 题型:选择题
一个直角三角形的模具,量得其中两边长分别为4cm、3cm,则第三条边长为( )
A.5cm B.4cm C. cm D.5cm或
cm D.5cm或 cm
cm
查看答案和解析>>
科目:初中数学 来源:2015届初中数学苏教版八年级上册期末复习练习卷(解析版) 题型:选择题
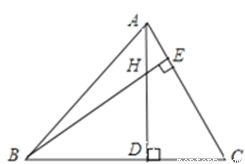
如图,已知△ABC中,∠ABC=45°,AC=4,H是高AD和BE的交点,则线段BH的长度为( )
A.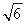 B.
B.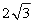 C.5 D.4
C.5 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com