
如图,矩形OABC的顶点A在y轴上,C在x轴上,双曲线y=
 与AB交于点D,与BC交于点E,DF⊥x轴于点F,EG⊥y轴于点G,交DF于点H.若矩形OGHF和矩形HDBE的面积分别是1和2,则k的值为( )
与AB交于点D,与BC交于点E,DF⊥x轴于点F,EG⊥y轴于点G,交DF于点H.若矩形OGHF和矩形HDBE的面积分别是1和2,则k的值为( )


A.
 B.
B.
 +1 C.
+1 C.
 D.2
D.2

B【考点】反比例函数系数k的几何意义.
【专题】计算题.
【分析】设D(t,
 ),由矩形OGHF的面积为1得到HF=
),由矩形OGHF的面积为1得到HF=
 ,于是根据反比例函数图象上点的坐标特征可表示出E点坐标为(kt,
,于是根据反比例函数图象上点的坐标特征可表示出E点坐标为(kt,
 ),接着利用矩形面积公式得到(kt﹣t)•(
),接着利用矩形面积公式得到(kt﹣t)•(
 ﹣
﹣
 )=2,然后解关于k的方程即可得到满足条件的k的值.
)=2,然后解关于k的方程即可得到满足条件的k的值.
【解答】解:设D(t,
 ),
),
∵矩形OGHF的面积为1,DF⊥x轴于点F,
∴HF=
 ,
,
而EG⊥y轴于点G,
∴E点的纵坐标为
 ,
,
当y=
 时,
时,
 =
=
 ,解得x=kt,
,解得x=kt,
∴E(kt,
 ),
),
∵矩形HDBE的面积为2,
∴(kt﹣t)•(
 ﹣
﹣
 )=2,
)=2,
整理得(k﹣1)2=2,
而k>0,
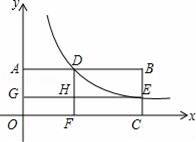
∴k=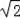
 +1.
+1.
故选B.

【点评】本题考查了反比例函数比例系数k的几何意义:在反比例函数y=
 图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.


科目:初中数学 来源: 题型:
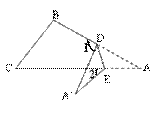
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外部时,则 与
与 和
和 之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )
之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )
A. B.
B.
C. D.
D.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,四个几何体分别为长方体、圆柱体、球体和三棱柱,这四个几何体中有三个的某一种视图都是同一种几何图形,则另一个几何体是( )
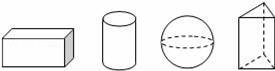

A.长方体 B.圆柱体 C.球体 D.三棱柱
查看答案和解析>>
科目:初中数学 来源: 题型:
对于函数y= - ,下列结论错误的是 ( )
,下列结论错误的是 ( )
A、当x>0时,y随x的增大而增大
B、当x<0时,y随x的增大而增大
C、当x=1时的函数值大于x= -1时的函数值
D、在函数图象所在的象限内,y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
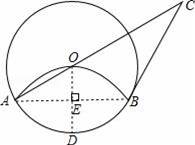
如图,将圆形纸片沿弦AB折叠后,圆弧恰好能经过圆心O,⊙O的切线BC与AO延长线交于点C.
(1)若⊙O半径为6cm,用扇形OAB围成一个圆锥的侧面,求这个圆锥的底面圆半径.
(2)求证:AB=BC.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com