
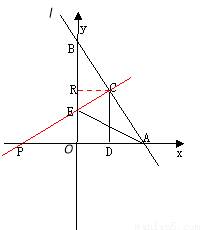
如图,直线 :
: 分别与
分别与 轴、
轴、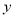 轴交于A、B两点,点C线段AB上,作CD⊥x轴于D, CD=2OD, 点E线段OB上,且AE=BE;
轴交于A、B两点,点C线段AB上,作CD⊥x轴于D, CD=2OD, 点E线段OB上,且AE=BE;


(1)填空:点C的坐标为( , );点E的坐标为( , );
(2)直线 过点E,且将△AOB分成面积比为1:2的两部分,求直线
过点E,且将△AOB分成面积比为1:2的两部分,求直线 的表达式;
的表达式;
(3)点P在x轴上运动,
①当PC+PE取最小值时,求点P的坐标及PC+PE的最小值;
②当PC-PE取最大值时,求点P的坐标及PC-PE的最大值;
见解析
【解析】
试题分析:(1)根据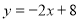 求出点A,B的坐标,A(4,0),B(0,8),所以OA=4,OB=8,设OD=m,则CD=2OD=2m,因为 CD⊥x轴,所以点C的坐标是(m,2m)代入
求出点A,B的坐标,A(4,0),B(0,8),所以OA=4,OB=8,设OD=m,则CD=2OD=2m,因为 CD⊥x轴,所以点C的坐标是(m,2m)代入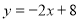 可求出点C的坐标,设OE=X,则AE=BE=8-x,在△OAE中,根据勾股定理可求出x的值,从而可得点E的坐标;(2)设直线m的表达式为
可求出点C的坐标,设OE=X,则AE=BE=8-x,在△OAE中,根据勾股定理可求出x的值,从而可得点E的坐标;(2)设直线m的表达式为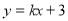 ,然后分情况讨论(3)①求出点E关于X轴的对称点E′坐标,然后求直线C E′与x轴的交点,即为点P;②直线CE与与x轴的交点即为点P.
,然后分情况讨论(3)①求出点E关于X轴的对称点E′坐标,然后求直线C E′与x轴的交点,即为点P;②直线CE与与x轴的交点即为点P.
试题解析:(1)点C( 2 , 4 );点E( 0 , 3 );
(2)设直线m的表达式为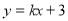
①如图:当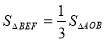 时,
时,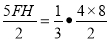
得FH=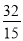 ,将
,将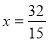 代入
代入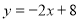 得
得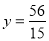
将点F(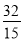 ,
,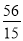 )代入
)代入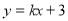 得
得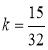 ,
,
所以直线m的表达式为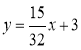
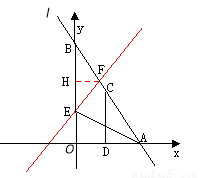
②如图:当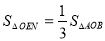 时,
时,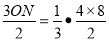 ,
,
得ON=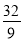 ,将点N(
,将点N(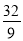 ,
,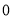 )代入
)代入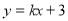 得
得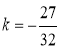 ,
,
所以直线m的表达式为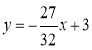
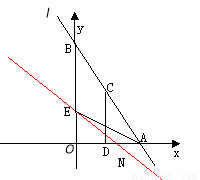
(3)①如图:E关于X轴的对称点E′坐标为(0,-3),
设直线CE′的表达式为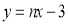 代入C(2,4)得;
代入C(2,4)得;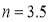 ,所以
,所以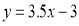
将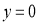 代入
代入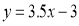 得
得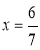
所以P的坐标为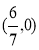
作E′Q⊥CD于Q,则CQ=OD=2,CQ=7
所以PC+PE的最小值= CE′=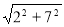 =
=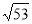
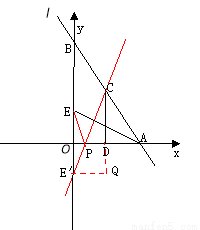
②如图:设直线CE的表达式为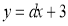 ,与x轴相交为p,
,与x轴相交为p,
代入C(2,4),得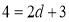 ,
,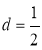
所以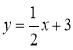 ,当
,当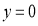 时,
时,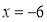 ;点P坐标为(-6,0),
;点P坐标为(-6,0),
作CR⊥y轴于R,则CR=OD=2,ER=1,
所以PC-PE的最大值= CE=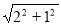 =
=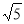
考点:1.一次函数与坐标轴的交点;2.求一次函数解析式;3.勾股定理;4.轴对称-最短距离.


科目:初中数学 来源:2014-2015学年福建省、三中、城关小学九年级上学期期中联考数学试卷(解析版) 题型:选择题
下列图形中,是中心对称图形,但不是轴对称图形的是( ).
A.正方形 B.矩形 C.菱形 D.平行四边形
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省泉州市惠安第三教研片区九年级上学期期中考试数学试卷(解析版) 题型:填空题
在比例尺为1:1000000的地图上,量得甲、乙两地的距离约为3厘米,则甲、乙两地的实际距离约为 千米.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省漳州立人学校八年级上学期期中考试数学试卷(解析版) 题型:选择题
点A(2,-3)关于y轴的对称点坐标是( )
A.(2,3) B.(-2,3) C.(-2,-3) D.(-3,2)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省九年级上学期期中质量监测数学试卷(解析版) 题型:选择题
不能判定四边形ABCD是平行四边形的条件是( )
A.∠A=∠C ∠B=∠D
B.AB∥CD AD=BC
C.AB∥CD ∠A=∠C
D.AB∥CD AB=CD
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省九年级上学期期中质量监测数学试卷(解析版) 题型:选择题
如图,在Rt⊿ABC中,∠C=90°, ∠B=22.5°, DE 垂直平分AB交BC于E, 若BE= , 则AC=( )
, 则AC=( )

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省龙岩市八年级上学期半期考试数学试卷(解析版) 题型:选择题
如图,在ΔABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=4,则CH的长为( )

A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com