
分析 (1)设里料的单价为x元/米,面料的单价为(2x+10)元/米,根据成本为76元列方程求解即可;
(2)设打折数为m,根据利润大于等于30元列不等式求解即可;
(3)设vip客户享受的降价率为x,然后根据VIP客户与普通用户批发件数相同列方程求解即可.
解答 解:(1)设里料的单价为x元/米,面料的单价为(2x+10)元/米.
根据题意得:0.8x+1.2(2x+10)=76.
解得:x=20.
2x+10=2×20+10=50.
答:面料的单价为50元/米,里料的单价为20元/米.
(2)设打折数为m.
根据题意得:150×$\frac{m}{10}$-76-14≥30.
解得:m≥8.
∴m的最小值为8.
答:m的最小值为8.
(3)150×0.8=120元.
设vip客户享受的降价率为x.
根据题意得:$\frac{9120}{120×(1-x)}=\frac{10080}{120(1+x)}$,
解得:x=0.05
经检验x=0.05是原方程的解.
答;vip客户享受的降价率为5%.
点评 本题主要考查的是一元一次方程、一元一次不等式、分式方程的应用,找出题目的相等关系和不等关系是解题的关键.


科目:初中数学 来源: 题型:解答题
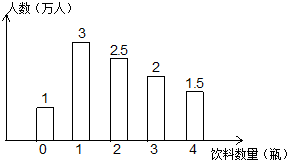 某环保小组为了解2010年上海世博会世博园的游客在园区内购买瓶装饮料数量的情况,一天,他们分别在A、B、C三个出口处,对离开园区的游客进行调查,其中在A出口调查所得的数据整理后绘成图.
某环保小组为了解2010年上海世博会世博园的游客在园区内购买瓶装饮料数量的情况,一天,他们分别在A、B、C三个出口处,对离开园区的游客进行调查,其中在A出口调查所得的数据整理后绘成图.| 出 口 | B | C |
| 人均购买饮料数量(瓶) | 3 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 37×104 | B. | 3.7×104 | C. | 0.37×106 | D. | 3.7×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
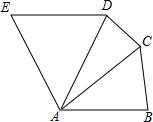 如图,在五边形ABCDE中,AB=AC=AD=AE,且AB∥ED,∠EAB=120°,则∠DCB=( )
如图,在五边形ABCDE中,AB=AC=AD=AE,且AB∥ED,∠EAB=120°,则∠DCB=( )| A. | 150° | B. | 160° | C. | 130° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
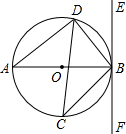 如图,⊙O的直径AB的长为10,弦BD的长为6,点C为$\widehat{AB}$上的一点,过点B的切线EF,连接AD,CD,CB;
如图,⊙O的直径AB的长为10,弦BD的长为6,点C为$\widehat{AB}$上的一点,过点B的切线EF,连接AD,CD,CB;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com