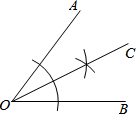
如图.用直尺和圆规作一个角的平分线.是运用了“全等三角形的对应角相等这一性质.由作图所得条件.判定三角形全等运用的方法是( )A．SSSB．ASAC．AASD．SAS 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

18．

如图，用直尺和圆规作一个角的平分线，是运用了“全等三角形的对应角相等”这一性质，由作图所得条件，判定三角形全等运用的方法是（　　）

A．

SSS

B．

ASA

C．

AAS

D．

SAS

分析熟练掌握三角形全等的判定条件是解答此题的关键．易知：OB=OA，BC=AC，OC=OC，因此符合SSS的条件．

解答解：连接BC，AC，
由作图知：在△OAC和△OBC中，
∵$\left\{\begin{array}{l}{AO=BO}\\{CO=CO}\\{AC=BC}\end{array}\right.$，
∴△OAC≌△OBC（SSS），
故选A．

点评本题考查的是作图-基本作图，要清楚作图时作出的线段OB与OA、BC与AC是相等的．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

5．观察下面三行数：
①-3，9，-27，81，-243，…；
②-5，7，-29，79，-245，…；
③-1，3，-9，27，-81，…．
（1）用乘方的形式表示第①行数中的第2016个数；
（2）第②、③行数与第①行数分别有什么关系？
（3）分别取这每行数的第10个数，计算这三个数的和．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

9．已知a²-8a+b-2$\sqrt{3b}$+|c-5|+19=0，求a，b，c的值．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

6．已知ab=-3，a+b=2，则a³b+ab³的值为-30．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

13．阅读下面的一段文字．
设$\frac{a}{b}$=$\frac{c}{d}$=…=$\frac{m}{n}$=k，则有a=bk，c=dk，…，m=nk，当b+d+…+n≠0时，$\frac{a+c+…+m}{b+d+…+n}$=$\frac{bk+dk+…+nk}{b+d+…+n}$=$\frac{（b+d+…+n）k}{（b+d+…+n）}$=k=$\frac{a}{b}$．
（1）你得到的结论是什么？
（2）利用（1）中的结论完成下题：在△ABC和△A′B′C′中，$\frac{AB}{A′B′}$=$\frac{BC}{B′C′}$=$\frac{CA}{C′A′}$=$\frac{3}{5}$，且△A′B′C′的周长是50cm，求△ABC的周长．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

3．

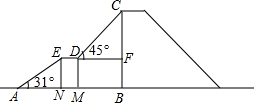如图，是某儿童乐园为小朋友设计的滑梯平面图．已知BC=5米，AB=8米，中间平台宽度DE=1米，EN、DM、CB为三根垂直于AB的支柱，垂足分别为N、M、B，∠EAB=31°，DF⊥BC于F，∠CDF=45°．求DM和BC的水平距离BM的长度．（结果精确到0.1米，参考数据：sin31°≈0.52，cos31°≈0.86，tan31°≈0.60）