
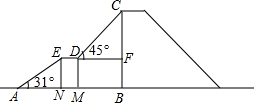
 如图,是某儿童乐园为小朋友设计的滑梯平面图.已知BC=5米,AB=8米,中间平台宽度DE=1米,EN、DM、CB为三根垂直于AB的支柱,垂足分别为N、M、B,∠EAB=31°,DF⊥BC于F,∠CDF=45°.求DM和BC的水平距离BM的长度.(结果精确到0.1米,参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
如图,是某儿童乐园为小朋友设计的滑梯平面图.已知BC=5米,AB=8米,中间平台宽度DE=1米,EN、DM、CB为三根垂直于AB的支柱,垂足分别为N、M、B,∠EAB=31°,DF⊥BC于F,∠CDF=45°.求DM和BC的水平距离BM的长度.(结果精确到0.1米,参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60) 分析 设BM=x米,在Rt△CDF中由∠CDF=45°可得CF=DF=x,则BF=EN=5-x,再由AB=8、MN=DE=1、BM=x得AN=7-x,最后在Rt△AEN中由∠EAB=31°根据EN=AN•tan31°列出关于x的方程,解之可得.
解答 解:设BM=x米.
∵∠CDF=45°,∠CFD=90°,
∴CF=DF=x米,
∴BF=BC-CF=(5-x)米.
∴EN=DM=BF=(5-x)米.
∵AB=8米,DE=1米,BM=DF=x米,
∴AN=AB-MN-BM=(7-x)米.
在△AEN中,∠ANE=90°,∠EAN=31°,
∴EN=AN•tan31°.
即5-x=(7-x)×0.6,
解得:x=2,
即DM和BC的水平距离BM的长度为2米.
点评 本题主要考查解直角三角形的应用,解直角三角形的一般过程是:
①将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题).
②根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:填空题
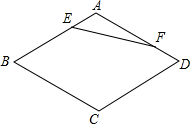 如图,在菱形ABCD中,∠B=60°,AB=a,点E,F分别是边AB,AD上的动点,且AE+AF=a,则线段EF的最小值为$\frac{\sqrt{3}}{2}$a.
如图,在菱形ABCD中,∠B=60°,AB=a,点E,F分别是边AB,AD上的动点,且AE+AF=a,则线段EF的最小值为$\frac{\sqrt{3}}{2}$a.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
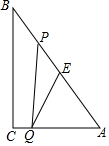 如图,Rt△ABC中,∠C=90°,BC=8cm,AC=6cm.点P从 B出发沿BA向A运动,速度为每秒1cm,点E是点B以P为对称中心的对称点,点P运动的同时,点Q从A出发沿AC向C运动,速度为每秒2cm,当 点Q到达顶点C时,P,Q同时停止运动,设P,Q两点运动时间为t秒.
如图,Rt△ABC中,∠C=90°,BC=8cm,AC=6cm.点P从 B出发沿BA向A运动,速度为每秒1cm,点E是点B以P为对称中心的对称点,点P运动的同时,点Q从A出发沿AC向C运动,速度为每秒2cm,当 点Q到达顶点C时,P,Q同时停止运动,设P,Q两点运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
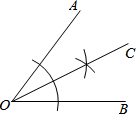 如图,用直尺和圆规作一个角的平分线,是运用了“全等三角形的对应角相等”这一性质,由作图所得条件,判定三角形全等运用的方法是( )
如图,用直尺和圆规作一个角的平分线,是运用了“全等三角形的对应角相等”这一性质,由作图所得条件,判定三角形全等运用的方法是( )| A. | SSS | B. | ASA | C. | AAS | D. | SAS |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com