
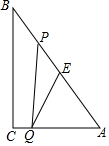
 如图,Rt△ABC中,∠C=90°,BC=8cm,AC=6cm.点P从 B出发沿BA向A运动,速度为每秒1cm,点E是点B以P为对称中心的对称点,点P运动的同时,点Q从A出发沿AC向C运动,速度为每秒2cm,当 点Q到达顶点C时,P,Q同时停止运动,设P,Q两点运动时间为t秒.
如图,Rt△ABC中,∠C=90°,BC=8cm,AC=6cm.点P从 B出发沿BA向A运动,速度为每秒1cm,点E是点B以P为对称中心的对称点,点P运动的同时,点Q从A出发沿AC向C运动,速度为每秒2cm,当 点Q到达顶点C时,P,Q同时停止运动,设P,Q两点运动时间为t秒.分析 (1)先在Rt△ABC中,由勾股定理求出AB=10,再由BP=t,AQ=2t,得出AP=10-t,然后由PQ∥BC,根据平行线分线段成比例定理得出$\frac{AP}{AB}=\frac{AQ}{AC}$,列出比例式=$\frac{10-t}{10}=\frac{2t}{6}$,求解即可;
(2)根据S四边形PQCB=S△ACB-S△APQ=$\frac{1}{2}$AC•BC-$\frac{1}{2}$AP•AQ•sinA,即可得出y关于t的函数关系式;根据四边形PQCB面积是△ABC面积的$\frac{3}{5}$,列出方程$\frac{4}{5}$t2-8t+24=$\frac{3}{4}$×24,解方程即可;
(3)△AEQ为等腰三角形时,分三种情况讨论:①AE=AQ;②EA=EQ;③QA=QE,每一种情况都可以列出关于t的方程,解方程即可.
解答 解:(1)Rt△ABC中,∵∠C=90°,BC=8cm,AC=6cm,
∴AB=10cm.
∵BP=t,AQ=2t,
∴AP=AB-BP=10-t.
∵PQ∥BC,
∴$\frac{AP}{AB}=\frac{AQ}{AC}$,
∴$\frac{10-t}{10}=\frac{2t}{6}$,
解得t=$\frac{30}{13}$;
(2)∵S四边形PQCB=S△ACB-S△APQ=$\frac{1}{2}$AC•BC-$\frac{1}{2}$AP•AQ•sinA
∴y=$\frac{1}{2}$×6×8-$\frac{1}{2}$×(10-t)•2t•$\frac{8}{10}$=24-$\frac{4}{5}$t(10-t)
=$\frac{4}{5}$t2-8t+24,
即y关于t的函数关系式为y=$\frac{4}{5}$t2-8t+24;
∵四边形PQCB面积能是△ABC面积的$\frac{3}{5}$,
∴$\frac{4}{5}$t2-8t+24=$\frac{3}{5}$×24,
整理,得t2-10t+12=0,
解得t1=5-$\sqrt{13}$,t2=5+$\sqrt{13}$(不合题意舍去).
故四边形PQCB面积能是△ABC面积的$\frac{3}{5}$,此时t的值为5-$\sqrt{13}$;
(3)△AEQ为等腰三角形时,分三种情况讨论:
①如果AE=AQ,那么10-2t=2t,解得t=$\frac{5}{2}$;
②如果EA=EQ,那么(10-2t)×$\frac{6}{10}$=t,解得t=$\frac{30}{11}$;
③如果QA=QE,那么2t×$\frac{6}{10}$=5-t,解得t=$\frac{25}{11}$.
故当t为$\frac{5}{2}$秒$\frac{30}{11}$秒$\frac{25}{11}$秒时,△AEQ为等腰三角形.
点评 此题是几何变换综合题,主要考查了勾股定理,平行线的判定,四边形的面积,等腰三角形的判定,中心对称的性质,综合性较强,难度适中.运用分类讨论、方程思想是解题的关键.


科目:初中数学 来源: 题型:解答题
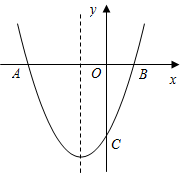 已知:抛物线的对称轴为x=-1,与x轴交于A,B两点,与y轴交于点C,其中A(-3,0)、C(0,-2).
已知:抛物线的对称轴为x=-1,与x轴交于A,B两点,与y轴交于点C,其中A(-3,0)、C(0,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB、AC是⊙O的切线,B、C为切点,过点O作AB的平行线交AC于点D,DE⊥AB于点E.
如图,AB、AC是⊙O的切线,B、C为切点,过点O作AB的平行线交AC于点D,DE⊥AB于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
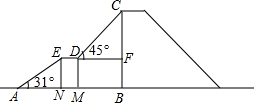 如图,是某儿童乐园为小朋友设计的滑梯平面图.已知BC=5米,AB=8米,中间平台宽度DE=1米,EN、DM、CB为三根垂直于AB的支柱,垂足分别为N、M、B,∠EAB=31°,DF⊥BC于F,∠CDF=45°.求DM和BC的水平距离BM的长度.(结果精确到0.1米,参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
如图,是某儿童乐园为小朋友设计的滑梯平面图.已知BC=5米,AB=8米,中间平台宽度DE=1米,EN、DM、CB为三根垂直于AB的支柱,垂足分别为N、M、B,∠EAB=31°,DF⊥BC于F,∠CDF=45°.求DM和BC的水平距离BM的长度.(结果精确到0.1米,参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com