
【题目】如果等式(x﹣3)2x﹣1=1,则x= .
【答案】![]() 或4
或4
【解析】解:①若2x﹣1=0, 解得x= ![]() ,
,
此时x﹣3=﹣2 ![]() ,
,
所以,x= ![]() 符合,
符合,
②若x﹣3=1,
解得x=4,
③若x﹣3=﹣1,
解得x=2,
此时2x﹣1=3,
所以,x=2符合,
综上所述,x= ![]() 或4.
或4.
所以答案是: ![]() 或4.
或4.
【考点精析】关于本题考查的零指数幂法则和有理数的乘方,需要了解零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);有理数乘方的法则:1、正数的任何次幂都是正数2、负数的奇次幂是负数;负数的偶次幂是正数;注意:当n为正奇数时: (-a)n=-an或(a -b)n=-(b-a)n , 当n为正偶数时: (-a)n =an 或 (a-b)n=(b-a)n才能得出正确答案.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:

组号 | 分组 | 频数 |
一 | 6≤m<7 | 2 |
二 | 7≤m<8 | 7 |
三 | 8≤m<9 | a |
四 | 9≤m≤10 | 2 |
(1)求a的值.
(2)若用扇形统计图来描述,求分数在8≤m<9内所对应的扇形的圆心角的度数.
(3)将在第一组内的两名选手记为A1,A2,在第四组内的两名选手记为B1,B2, 从第一组和第四组中随机选取2名选手进行调研座谈,求第一组至少有1名选手被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为了响应国家阳光体育活动,选派部分学生参加足球、乒乓球、篮球、排球队集训.根据参加项目制成如下两幅不完整的统计图(要求每位同学只能选择一种自己喜欢的球类,图中用足球、乒乓球、篮球、排球代表喜欢这四种球类某种球类的学生人数,请你根据图中提供的信息解答下列问题:
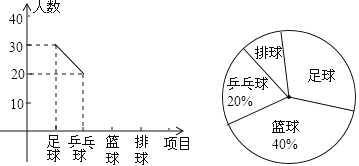
(1)参加篮球队的有 人,参加足球队的人数占全部参加人数的 %.
(2)喜欢排球队的人数在扇形统计图中所占的圆心角是多少度?并补全频数分布折线统计图.
(3)若足球队只剩一个集训名额,学生小明和小虎都想参加足球队,决定采用随机摸球的方式确定参加权,具体规则如下:一个不透明的袋子中装着标有数字1、2、3、4的四个完全相同的小球,小明随机地从四个小球中摸出一球然后放回,小虎再随机地摸出一球,若小明摸出的小球标有数字比小虎摸出的小球标有的数字大,则小明参加;若小明摸出的小球标有数字比小虎摸出的小球标有的数字小,则小虎参加,试分析这种规则对双方是否公平?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(a,0)、B(b,0),且(a+4)2+|b﹣2|=0. 
(1)求a、b的值.
(2)在y轴的正半轴上找一点C,使得三角形ABC的面积是15,求出点C的坐标.
(3)过(2)中的点C作直线MN∥x轴,在直线MN上是否存在点D,使得三角形ACD的面积是三角形ABC面积的 ![]() ?若存在,求出点D的坐标;若不存在,请说明理由.
?若存在,求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E、F分别在边BC、CD上,且AE=EF=FA.下列结论:①△ABE≌△ADF;②CE=CF;③∠AEB=75°;④BE+DF=EF;⑤S△ABE+S△ADF=S△CEF , 其中正确的是①②③⑤(只填写序号). 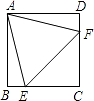
查看答案和解析>>
科目:初中数学 来源: 题型:
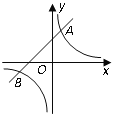
【题目】如图,反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点.
两点.
(1)求反比例函数与一次函数的解析式;
(2)根据图象回答:当![]() 取何值时,反比例函数的值大于一次函数的值.
取何值时,反比例函数的值大于一次函数的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() .
.
(1)若该反比例函数的图象与直线![]() (
(![]() ≠0)只有一个公共点,求
≠0)只有一个公共点,求![]() 的值;
的值;
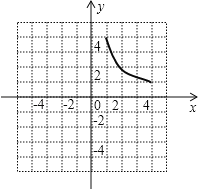
(2)如图,反比例函数![]() 的图象记为曲线
的图象记为曲线![]() ,将
,将![]() 向左平移2个单位长度,得曲线
向左平移2个单位长度,得曲线![]() ,请在图中画出
,请在图中画出![]() ,并直接写出
,并直接写出![]() 平移至
平移至![]() 处 所扫过的面积.
处 所扫过的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com