
 ),此抛物线的顶点为D.
),此抛物线的顶点为D.
 ,OA=3得到∠ABE=30°,
,OA=3得到∠ABE=30°, ,OB=1得到∠CBO=60°,则∠CBE=∠CBO+∠ABE=60°+30°=90°因而ABEC是矩形.
,OB=1得到∠CBO=60°,则∠CBE=∠CBO+∠ABE=60°+30°=90°因而ABEC是矩形. ),
),

 ,
, .
. ),
), ).
).
 ,OA=3,
,OA=3, ,OB=1,
,OB=1,
 )的对称点A1(3,2
)的对称点A1(3,2 ).
). )
)
 )、D(-1,
)、D(-1, )
)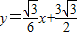 .
. ,
, ,
, ).
).

 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源:2009年北京市大兴区中考数学二模试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2009年北京市大兴区中考数学二模试卷(解析版) 题型:解答题
 ,则电线杆AB的长为多少米?
,则电线杆AB的长为多少米?
查看答案和解析>>
科目:初中数学 来源:2009年北京市大兴区中考数学二模试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com