解:(1)A′(-4,0),B′(0,2).
(2)设经过A'、B的抛物线的解析式为y=a(x+4)(x-2),由于抛物线过B′(0,2),
可得:2=a×4×(-2),
因此a=-

.
∴二次函数的解析式为:y=-

(x+4)(x-2)=-

x
2-

x+2
(3)顶点M不在直线AA′上,理由如下:
由(2)可知,抛物线的顶点为M(-1,

).
直线AA'对应的一次函数解析式为y=x+4,
而-1+4≠

,故顶点M不在直线AA′上.
分析:(1)根据旋转的角度可知A′、B′分别在x的负半轴和y的正半轴上,而A′的横坐标的绝对值就是A的纵坐标,B′的纵坐标就是B的横坐标.由此可得出A′、B′的坐标.
(2)根据(1)得出的A′、B′的坐标,以及已知的B的坐标,可用待定系数法求出二次函数的解析式.
(3)根据(2)的函数式即可求出其顶点坐标,然后用待定系数法求出AA′的解析式,然后判断二次函数的顶点是否在AA′所在的直线上即可.
点评:本题主要考查了用待定系数法求二次函数和一次函数的方法.根据旋转的性质得出A′、B′的坐标是解题的基础.

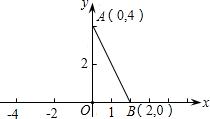 ′OB′.
′OB′. .
. (x+4)(x-2)=-
(x+4)(x-2)=- x2-
x2- x+2
x+2 ).
). ,故顶点M不在直线AA′上.
,故顶点M不在直线AA′上.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案 =2,∠ADC=30°
=2,∠ADC=30°