
【题目】如图,已知抛物线y=![]() x2+mx+n与x轴相交于点A、B两点,过点B的直线y=x+b交抛物线于另一点C(-5,6),点D是线段BC上的一个动点(点D与点B、C不重合),作DE∥AC,交该抛物线于点E,
x2+mx+n与x轴相交于点A、B两点,过点B的直线y=x+b交抛物线于另一点C(-5,6),点D是线段BC上的一个动点(点D与点B、C不重合),作DE∥AC,交该抛物线于点E,
(1)求m,n,b的值;
(2)求tan∠ACB;
(3)探究在点D运动过程中,是否存在∠DEA=45°,若存在,则求此时线段AE的长;若不存在,请说明理由.

【答案】(1)m=1,n=![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】分析:(1)由点C的坐标利用待定系数法即可求出一次函数解析式中的常数项b,再令一次函数解析式中y=0求出x值,由此可得出点B的坐标,由点B、C的坐标利用待定系数法即可求出二次函数解析式中的系数m、n;
(2)过点C作CF⊥x轴于点F,过点A作AG⊥BC于点G,由二次函数解析式可求出交点A、B的坐标,由点B、C、A点的坐标,可找出线段CF、BF、AF、BA的长,通过解直角三角形即可找出BG、AG、BC的长,再根据正切的计算公式即可得出结论;
(3)假设存在,连接AE,过点E作EM⊥x轴于点M,通过角的计算得出∠BAE=∠BDE=∠BCA,设出点E的坐标,根据(2)的结论tan∠ACB=![]() ,即可得出关于t的一元二次方程,解方程即可得出结论.
,即可得出关于t的一元二次方程,解方程即可得出结论.
详解:(1)∵直线y=x+b经过点C(5,6) ∴b=1
∵B在x轴上,且在直线y=x+b上 ∴B(1,0)
∵抛物线y=![]() x2+mx+n过B(1,0)、C(5,6)
x2+mx+n过B(1,0)、C(5,6)
∴ m=1,n=![]()
(2)作CF⊥x轴于F,作AG⊥BC于G
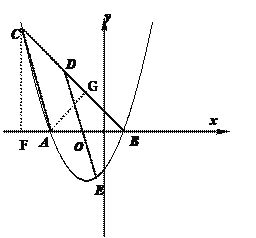
∴F(5,0)
∵抛物线y=![]() x2+mx+n与x轴交于A、B
x2+mx+n与x轴交于A、B
∴A(3,0) B(1,0)∴CF=BF=6,AF=2,AB=4∴∠CBF=45°,BC=6![]() ,
,
∴BG=AG=2![]() ∴CG=4
∴CG=4![]()
∴tan∠ACB=![]()
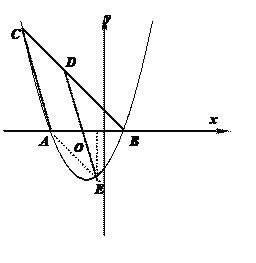
(3) ∵DE∥AC ∴∠BDE=∠BCA∵∠DEA=45° ∠DBA=45°
∴∠BAE=∠BDE=∠BCA
∴tan∠BAE=![]()
设E(t, ![]() t2+t
t2+t![]() ) ∴tan∠BAE=
) ∴tan∠BAE=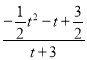 =
=![]()
∴t=0 ∴E(0, ![]() ) ∴AE=
) ∴AE=![]()


科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接AD.
(1)AB=_____;
(2)当∠D=20°时,求∠BOD的度数.
(3)若△ACD与△BCO相似,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为6cm 的⊙O中,C,D为直径AB 的三等分点,点E,F分别在AB两侧的半圆上,∠BCE =∠BDF = 60°,连结AE,BF.则图中两个阴影部分的面积和为 cm2.

查看答案和解析>>
科目:初中数学 来源: 题型:
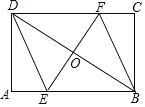
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() .将
.将![]() 沿
沿![]() 对折至
对折至![]() ,延长
,延长![]() 交边
交边![]() 于点
于点![]() .连结
.连结![]() 、
、![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() 是正三角形;④
是正三角形;④![]() 的面积为90.其中正确的是______(填所有正确答案的序号).
的面积为90.其中正确的是______(填所有正确答案的序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E,F分别在BC,CD上,三角形AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②AG=2GC,③BE+DF=EF,④S△CEF=2S△ABE正确的有_____(只填序号).
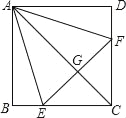
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 上一点,且
上一点,且![]() ,过点
,过点![]() 分别作
分别作![]() ,
,![]() ,垂足分别是
,垂足分别是![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() 是
是![]() 的中点;③
的中点;③![]() 垂直平分
垂直平分![]() ;④
;④![]() ;其中正确的个数为( )
;其中正确的个数为( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC ,分别以AB 、AC 为边在△ABC 的外部作等边三角形ABD和等边三角形ACE联结DC 、BE 试说明DCBE的理由.
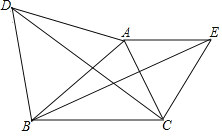
查看答案和解析>>
科目:初中数学 来源: 题型:
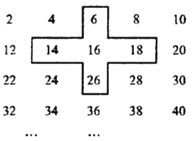
【题目】将连续的偶数2,4,6,8,…,如图所示排列:
(1)求图中十字框内5个数的和与中间的数16的倍数关系.
(2)若将十字框上下左右移动,可框住另外的五个数,请说明这五个数的和与十字框最中间的数之间存在的关系.
(3)若将十字框上下左右移动,框住的五个数的和能等于2019吗?若能,请写出这五个数;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com