
| 用水量/月 | 单价(元/m3) |
| 不超过20m3 | 3 |
| 超过20m3的部分 | 4 |
| 另:每立方米用水加收0.2元的城市污水处理费 | |
分析 (1)该用户1月份用水量没有超过20m3,直接用单价×用水量即可;
(2)设该用户2月份用水xm3,由题意,得20×3+4×(x-20)+0.2x=80,求出x的值即可;
(3)首先设出用户3月份实际用水am3,然后求出a的值,根据表格水价求出该用户3月份实际应该缴纳水费.
解答 解:(1)19×3.2=60.8(元),
答:该用户1月份应该缴纳水费60.8元;
(2)设该用户2月份用水x立方米,
20×3+(x-20)×4+0.2x=80,
解得:x=$\frac{500}{21}$,
答:该用户2月份用水$\frac{500}{21}$立方米;
(3)设该用户3月份实际用水am3.
因为58.8<20×3,所以该用户上交水费的单价为3.2元/m3.
由题意,得70%a×3.2=58.8.
解得:a=$\frac{105}{4}$.
因为$\frac{105}{4}$>20,
所以该用户3月份实际应该缴纳水费为:20×3.2+4.2×($\frac{105}{4}$-20)=90.25元.
答:该用户3月份实际应该缴纳水费90.25元.
点评 本题考查了一元一次方程的应用,关键是正确理解题意,找出题目中的等量关系,设出未知数,列出方程.


科目:初中数学 来源: 题型:选择题
| A. | 2.1(精确到0.1) | B. | 2.05(精确到百分位) | ||
| C. | 2.054(精确到0.001) | D. | 2.0544(精确到万分位) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
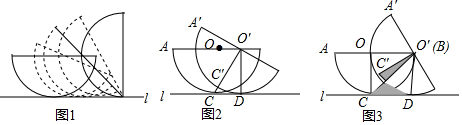 如图1,一个半径为2的半圆在平面作无滑动顺时针滚动,可以把平面看做直线l,初始位置的半圆O与直线l相切于点C,AB∥l,滚动过程中,半圆O′与直线l相切于点D,点A、B、C在半圆O′上的对应点分别为A′、B′、C′.
如图1,一个半径为2的半圆在平面作无滑动顺时针滚动,可以把平面看做直线l,初始位置的半圆O与直线l相切于点C,AB∥l,滚动过程中,半圆O′与直线l相切于点D,点A、B、C在半圆O′上的对应点分别为A′、B′、C′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,正比例函数y=2x与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,A点的横坐标为2,AC⊥x轴于点C,连接BC.
如图,在平面直角坐标系xOy中,正比例函数y=2x与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,A点的横坐标为2,AC⊥x轴于点C,连接BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
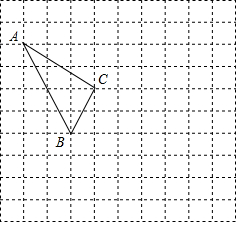 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图.已知二次函数y=ax2+bx(α≠0)经过点A(-2,0),B(-3,3).
如图.已知二次函数y=ax2+bx(α≠0)经过点A(-2,0),B(-3,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)与x轴交于A,B两点,与y轴交于点C,三个交点的坐标分别为A(-1,0),B(3,0),C(0,3).
如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)与x轴交于A,B两点,与y轴交于点C,三个交点的坐标分别为A(-1,0),B(3,0),C(0,3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com