
 ��ͼ����ƽ��ֱ������ϵxOy�У�����������y=2x�뷴��������y=$\frac{k}{x}$��ͼ����A��B���㣬A��ĺ�����Ϊ2��AC��x���ڵ�C������BC��
��ͼ����ƽ��ֱ������ϵxOy�У�����������y=2x�뷴��������y=$\frac{k}{x}$��ͼ����A��B���㣬A��ĺ�����Ϊ2��AC��x���ڵ�C������BC������ ��1����A�������������������������A�����꣬���뷴������������ʽ�����k������÷�������������ʽ��
��2������ͼ��������������ͼ���ڷ���������ͼ����·�������д��x��ȡֵ��Χ��
��3�������������B��C�����꣬������á�ABC��������ٽ�ϡ�OPC���ABC�����������P�����꣮
��� �⣺��1����x=2����y=2x�У���y=2��2=4��
���A������2��4����
�ߵ�A�ڷ���������y=$\frac{k}{x}$��ͼ���ϣ�
��k=2��4=8��
�෴���������Ľ���ʽΪy=$\frac{8}{x}$��
��2�����ݶԳ��Կ�֪B��-2��-4����
��ͼ���֪��-2��x��0��x��2ʱ��2x��$\frac{k}{x}$
��3����AC��OC��
��OC=2��
��A��B����ԭ��Գƣ�
��B��������-2��-4����
��B��OC�ľ���Ϊ4��
��S��ABC=2S��ACO=2��$\frac{1}{2}$��2��4=8��
��S��OPC=8��
��P������Ϊ��x��$\frac{8}{x}$������P��OC�ľ���Ϊ|$\frac{8}{x}$|��
��$\frac{1}{2}$��|$\frac{8}{x}$|��2=8�����x=1��-1��
��P��������1��8����-1��-8����
���� ������Ҫ�������ϵ������������ʽ�������Ľ������⡢�����ε������֪ʶ������Ĺؼ���������ô���ϵ����ȷ����������ʽ��ѧ������ͼ���������ȷ���Ա���ȡֵ��Χ�������п��������ͣ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
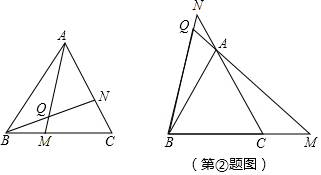
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
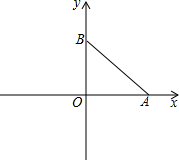 ��ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬A��B���������ֱ�Ϊ
��ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬A��B���������ֱ�Ϊ�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��ˮ��/�� | ���ۣ�Ԫ/m3�� |
| ������20m3 | 3 |
| ����20m3�IJ��� | 4 |
| ����ÿ��������ˮ����0.2Ԫ�ij�����ˮ������ | |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
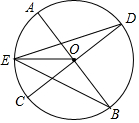 ��ͼ����֪��AB��CD�ǡ�O������ֱ����EΪ$\widehat{AC}$���е㣬��֤��EOƽ�֡�DEB��
��ͼ����֪��AB��CD�ǡ�O������ֱ����EΪ$\widehat{AC}$���е㣬��֤��EOƽ�֡�DEB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com