
分析 先根据根与系数的关系得出x1+x2=-$\frac{-\sqrt{6}}{2}$=$\frac{\sqrt{6}}{2}$,x1•x2=-$\frac{1}{2}$,
(1)根据完全平方公式进行变形,最后整体代入求出即可;
(2)根据完全平方公式进行变形,最后整体代入求出即可;
(3)根据多项式乘以多项式方程进行计算,最后整体代入求出即可.
解答 解:∵x1,x2是方程2x2-$\sqrt{6}$x-1=0的两个根,
∴x1+x2=-$\frac{-\sqrt{6}}{2}$=$\frac{\sqrt{6}}{2}$,x1•x2=-$\frac{1}{2}$,
(1)x12+x22;
=(x1+x2)2-2x1•x2=($\frac{\sqrt{6}}{2}$)2-2×(-$\frac{1}{2}$)=$\frac{5}{2}$;
(2)(x1-x2)2;
=(x1+x2)2-4x1•x2=($\frac{\sqrt{6}}{2}$)2-4×(-$\frac{1}{2}$)=$\frac{7}{2}$;
(3)(x1+$\frac{1}{{x}_{2}}$)(x2+$\frac{1}{{x}_{1}}$).
=x1x2+1+1+$\frac{1}{{x}_{1}{x}_{2}}$
=-$\frac{1}{2}$+2+$\frac{1}{-\frac{1}{2}}$
=-$\frac{1}{2}$.
点评 此题考查了一元二次方程根与系数的关系.x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$,反过来也成立,即$\frac{b}{a}$=-(x1+x2),$\frac{c}{a}$=x1x2,用了整体代入思想.


科目:初中数学 来源: 题型:解答题
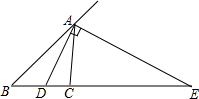 已知:AD、AE分别为△ABC的内、外角平分线,求证:$\frac{1}{BD}$+$\frac{1}{BE}$=$\frac{2}{BC}$.
已知:AD、AE分别为△ABC的内、外角平分线,求证:$\frac{1}{BD}$+$\frac{1}{BE}$=$\frac{2}{BC}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
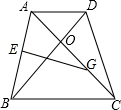 在等腰梯形ABCD中,AD∥BC,AB=CD,∠BOC=60°,对角线AC,BD相交于点O,点E,G分别为AB,OC的中点,连接EG.
在等腰梯形ABCD中,AD∥BC,AB=CD,∠BOC=60°,对角线AC,BD相交于点O,点E,G分别为AB,OC的中点,连接EG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
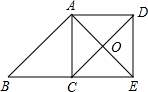 如图,?ABCD中,O为CD的中点,连接AO并延长,交BC延长线于E,连接AC,DE.
如图,?ABCD中,O为CD的中点,连接AO并延长,交BC延长线于E,连接AC,DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com