
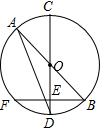
 已知直径CD⊥弦BF于 E,AB为?O的直径.
已知直径CD⊥弦BF于 E,AB为?O的直径.分析 (1)根据垂径定理得到$\widehat{FD}$=$\widehat{BD}$,根据圆心角、弧、弦的关系定理证明即可;
(2)根据圆周角定理得到∠BOD=2∠DAB,根据三角形内角和定理计算即可.
解答 (1)证明:∵直径CD⊥弦BF,
∴$\widehat{FD}$=$\widehat{BD}$,
∵∠AOC=∠BOD,
∴$\widehat{BD}$=$\widehat{AC}$,
∴$\widehat{FD}$=$\widehat{AC}$;
(2)解:由圆周角定理得,∠BOD=2∠DAB,
∵∠DAB=∠B,
∴∠BOD=2∠B,
∵CD⊥BF,
∴∠B=30°.
点评 本题考查的是圆心角、弧、弦的关系和圆周角定理的应用,掌握在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
 如图,将长方形ABCD沿直线BD折叠,使点C落在点E处,BE交AD于F,连接CE,下列结论①FA=FE ②BD平分∠FBC ③∠DEC=∠EBD ④EC垂直平分BD,正确的是( )
如图,将长方形ABCD沿直线BD折叠,使点C落在点E处,BE交AD于F,连接CE,下列结论①FA=FE ②BD平分∠FBC ③∠DEC=∠EBD ④EC垂直平分BD,正确的是( )| A. | ①② | B. | ①②③ | C. | ②③④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 用水量 | 单价 |
| 不超过6m3 | 2元/m3 |
| 超过6m3不到10m3 | 4元m3 |
| 超出10m3 | 8元m3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com