
| 用水量 | 单价 |
| 不超过6m3 | 2元/m3 |
| 超过6m3不到10m3 | 4元m3 |
| 超出10m3 | 8元m3 |
分析 (1)将不超出6m3部分的价格,超出6m3不超出10m3的价格,和超出10m3的价格相加,即为该用户居民2月份应交的水费;
(2)应分两种情况进行讨论,当3月份用水量不超过6m3时,列出方程进行求解,根据求解的结果进行验证;若结果小于6m3,符合题意,否则应舍去;当3月份的用水量超出6m3不超出10m3时,列出方程进行求解,同样进行验证.
解答 解:(1)应收水费2×6+4×(10-6)+8×(12.5-10)=48元.
(2)当三月份用水不超过6m3时,设三月份用水xm3,则2x+2×6+4×4+8(15-x-10)=44,
解得:x=4<6,符合题意.
15-4=11m3.
2x+12+8(15-x-10)=44,
当三月份用水超过6m3时,但不超过10m3时,设三月份用水xm3,则四月份超过6m3时,但不超过10m3时:无解(舍去).
所以三月份用水4m3,四月份用水11m3.
点评 本题主要考查一元一次方程的应用,在解题过程中应先情况进行讨论,根据求解的结果进行验证.


科目:初中数学 来源: 题型:解答题
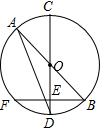 已知直径CD⊥弦BF于 E,AB为?O的直径.
已知直径CD⊥弦BF于 E,AB为?O的直径.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一农户要建一个矩形鸡舍,为了节省材料鸡舍的一边利用长为12米的墙,另外三边用长为25米的建筑材料围成,为方便进出,在垂直墙的一边留下一个宽1米的门,所围成矩形鸡舍的长、宽分别是多少时,鸡舍面积为80平方米?
如图,一农户要建一个矩形鸡舍,为了节省材料鸡舍的一边利用长为12米的墙,另外三边用长为25米的建筑材料围成,为方便进出,在垂直墙的一边留下一个宽1米的门,所围成矩形鸡舍的长、宽分别是多少时,鸡舍面积为80平方米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
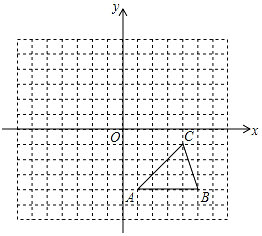 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.
如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 售出数量(件) | 7 | 6 | 3 | 5 | 4 | 5 |
| 售价(元) | +3 | +2 | +1 | 0 | -1 | -2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com