
【题目】如图,若点A在数轴上对应的数为a,点B在数轴上对应的数为b,且a,b满足|a+2|+(b﹣1)2=0.
![]()
(1)求线段AB的长;
(2)点C在数轴上对应的数为x,且x是方程2x﹣1=![]() x+2的解,在数轴上是否存在点P,使PA+PB=PC,若存在,直接写出点P对应的数;若不存在,说明理由;
x+2的解,在数轴上是否存在点P,使PA+PB=PC,若存在,直接写出点P对应的数;若不存在,说明理由;
(3)在(1)的条件下,将点B向右平移5个单位长度至点B’,此时在原点O处放一挡板,一小球甲从点A处以1个单位长度/秒的速度向左运动;同时另一小球乙从点B’处以2个单位长度/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),求甲、乙两小球到原点的距离相等时经历的时间.
【答案】(1)3;(2)存在;﹣3或﹣1;(3)![]() 秒或8秒.
秒或8秒.
【解析】
(1)根据绝对值及完全平方的非负性,可得出a、b的值,继而可得出线段AB的长;
(2)先求出x的值,再由PA+PB=PC,可得出点P对应的数.
(3)根据题意列方程,即可解答(3).
解(1)∵|a+2|+(b﹣1)2=0,
∴a=﹣2,b=1,
∴AB=b﹣a=1﹣(﹣2)=3.
(2)2x﹣1=![]() x+2,
x+2,
解得:x=2,
![]()
由题意得,点P只能在点B的左边,
①当点P在AB之间时,x+2+1﹣x=2﹣x,
解得:x=﹣1;
②当点P在A点左边时,﹣2﹣x+1﹣x=2﹣x,
解得:x=﹣3,
综上可得P所对应的数是﹣3或﹣1.
(3)①甲、乙两球均向左运动,即0≤t≤3时,
此时OA=2+t,OB’=6﹣2t,
则可得方程2+t=6﹣2t,
解得t=![]() ;
;
②甲继续向左运动,乙向右运动,即t>3时,
此时OA=2+t,OB’=2t﹣6,
则可得方程2+t=2t﹣6,
解得t=8.
答:甲、乙两小球到原点的距离相等时经历的时间为![]() 秒或8秒.
秒或8秒.


科目:初中数学 来源: 题型:
【题目】如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.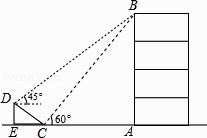
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上三点A,O,B表示的数分别为-3,0,1,点P为数轴上任意一点,其表示的数为x.
(1)如果点P到点A,点B的距离相等,那么x=______;
(2)若点P到点A,点B的距离之和最小,则整数x是____________ ;
(3)当点P到点A,点B的距离之和是6时,求x的值;
(4)若点P以每秒3个单位长度的速度从点O沿着数轴的负方向运动时,点E以每秒1个单位长度的速度从点A沿着数轴的负方向运动、点F以每秒4个单位长度的速度从点B沿着数轴的负方向运动,且三个点同时出发,那么运动多少秒时,点P到点E,点F的距离相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线a、b相交于点O,∠1=50°,点A在直线a上,直线b上存在点B,使以点O、A、B为顶点的三角形是等腰三角形,这样的B点有( ) 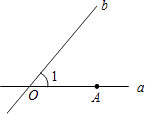
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用同样规格的黑白两种正方形瓷砖铺设正方形地面,观察图形并猜想填空:当黑色瓷砖为28块时,白色瓷砖块数为( )

A. 27 B. 28 C. 33 D. 35
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=AD,CB=CD,AB ∥ CD.
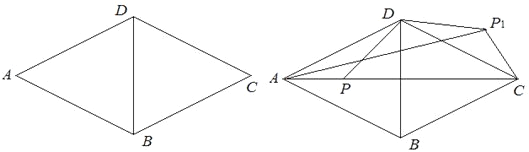
(1)求证:四边形ABCD是菱形.
(2)当△ABD满足什么条件时,四边形ABCD是正方形.(直接写出一个符合要求的条件).
(3)对角线AC和BD交于点O,∠ ADC =120°,AC=8, P为对角线AC上的一个动点,连接DP,将DP绕点D逆时针方向旋转120°得到线段DP1,直接写出A P1的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
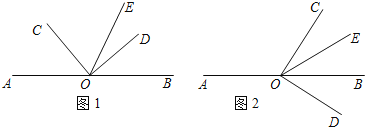
(1)如图(1),若∠AOC=![]() ,求∠DOE的度数;
,求∠DOE的度数;
(2)如图(2),将∠COD绕顶点O旋转,且保持射线OC在直线AB上方,在整个旋转过程中,当∠AOC的度数是多少时,∠COE=2∠DOB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com