
【题目】如图,四边形ABCD中,AB=AD,CB=CD,AB ∥ CD.
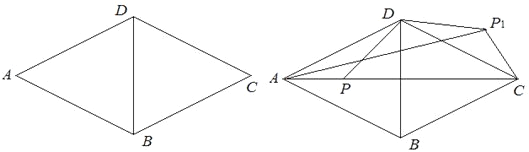
(1)求证:四边形ABCD是菱形.
(2)当△ABD满足什么条件时,四边形ABCD是正方形.(直接写出一个符合要求的条件).
(3)对角线AC和BD交于点O,∠ ADC =120°,AC=8, P为对角线AC上的一个动点,连接DP,将DP绕点D逆时针方向旋转120°得到线段DP1,直接写出A P1的取值范围.
【答案】(1)见解析;(2)见解析;(3) ![]() .
.
【解析】(1)先证明四边形ABCD是平行四边形,然后证明它是菱形即可.
(2)由(1)已知四边形ABCD是菱形,所以当△ABD是直角三角形时,四边形ABCD是正方形.
(3)将线段AC顺时针方向旋转60°得到线段CE,并连接AE,点到直线的距离垂线段最短,所以AP1垂直CE时,AP1取最小值,点P1在E点,AP1取最大值,即可求解.
证明:(1) AB=AD,CB=CD,∴∠ABD=∠ADB,∠CBD=∠CDB,
∵AB∥CD,∴∠ABD=∠CDB,∴∠ADB=∠CBD,
∴AD∥BC,∴四边形ABCD是平行四边形.
又∵AB=AD,∴四边形ABCD是菱形.
(2)要使四边形ABCD是正方形,则∠A=∠ABC=∠C=∠ADC=90°,
∴当△ABD是直角三角形时,即∠BAD=90°时,四边形ABCD是正方形;
(3)以点C为中心,将线段AC顺时针方向旋转60°得到线段CE,由题意可知,点P1在线段CE上运动.
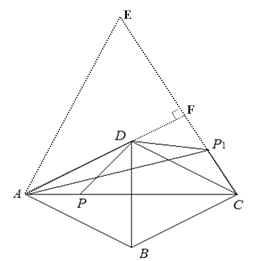
连接AE,
∵AC=CE,∠ACE=60°,∴△ACE为等边三角形,
∴AC=CE=AE=8,过点A作![]() 于点F,
于点F,
∴.![]() 当点P1在点F时,线段AP1最短,此时;
当点P1在点F时,线段AP1最短,此时;![]() .
.
当点P1在点E时,线段AP1最长,此时AP1=8,
.![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】同学们都知道:|5﹣(﹣2)|表示5与﹣2之差的绝对值,实际上也可理解为5与﹣2两数在数轴上所对应的两点之间的距离.请你借助数轴进行以下探索:
![]()
(1)数轴上表示5与﹣2两点之间的距离是
(2)数轴上表示x与2的两点之间的距离可以表示为 .
(3)同理|x+3|+|x﹣1|表示数轴上有理数x所对应的点到﹣3和1所对应的点的距离之和,请你找出所有符合条件的整数x,使得|x+3|+|x﹣1|=4,这样的整数是 .
(4)由以上探索猜想|x+10|+|x+2|+|x﹣8|是否有最小值?如果有,直接写出最小值;如果没有,说明理由.
(5)由以上探索猜想|x+10|+|x+2|+|x﹣8|+|x﹣10|是否有最小值?如果有,直接写出最小值;如果没有,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是工人师傅用同一种材料制成的金属框架,已知![]() ,
,![]() ,
,![]() ,其中
,其中![]() 的周长为24cm,
的周长为24cm,![]() ,则制成整个金属框架所需这种材料的总长度为( )
,则制成整个金属框架所需这种材料的总长度为( )

A. 45cm B. 48cm C. 51cm D. 54cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司与销售人员签订了这样的工资合同:工资由两部分组成,一部分是基本工资,每人每月3000元;另一部分是按月销售量确定的奖励工资,每销售一件产品,奖励工资10元.设某销售员销售产品x件,他应得工资记为y元.
(1)求y与x的函数关系式.
(2)该销售员的工资为4100元,他这个月销售了多少件产品?
(3)要使每月工资超过4500元,该月的销售量应当超过多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若点A在数轴上对应的数为a,点B在数轴上对应的数为b,且a,b满足|a+2|+(b﹣1)2=0.
![]()
(1)求线段AB的长;
(2)点C在数轴上对应的数为x,且x是方程2x﹣1=![]() x+2的解,在数轴上是否存在点P,使PA+PB=PC,若存在,直接写出点P对应的数;若不存在,说明理由;
x+2的解,在数轴上是否存在点P,使PA+PB=PC,若存在,直接写出点P对应的数;若不存在,说明理由;
(3)在(1)的条件下,将点B向右平移5个单位长度至点B’,此时在原点O处放一挡板,一小球甲从点A处以1个单位长度/秒的速度向左运动;同时另一小球乙从点B’处以2个单位长度/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),求甲、乙两小球到原点的距离相等时经历的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,∠BAC=90°,AB=AC,点E在AC上(且不与点A,C重合),在△ABC的外部作△CED,使∠CED=90°,DE=CE,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.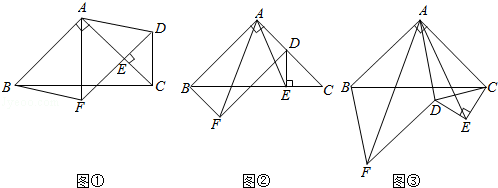
(1)请直接写出线段AF,AE的数量关系;
(2)将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
(3)在图②的基础上,将△CED绕点C继续逆时针旋转,请判断(2)问中的结论是否发生变化?若不变,结合图③写出证明过程;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣3x+3与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线y= ![]() (k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y=
(k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y= ![]() (k≠0)上的点D1处,则a= .
(k≠0)上的点D1处,则a= . 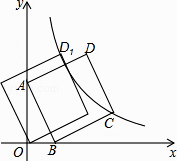
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB是直径,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E. 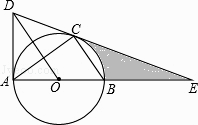
(1)求证:DE是⊙O的切线;
(2)若AE=6,CE=2 ![]() ,求线段CE、BE与劣弧BC所围成的图形面积.(结果保留根号和π)
,求线段CE、BE与劣弧BC所围成的图形面积.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解九年级学生体育测试情况,以九年级(1)班学生的体育测试成绩为样本,按A,B,C,D四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题: 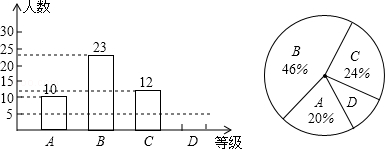
(说明:A级:90分~100分;B级:75分~89分;C级:60分~74分;D级:60分以下)
(1)九年级(1)班体育测试的人数为;
(2)请把条形统计图补充完整;
(3)扇形统计图中A级所在的扇形的圆心角度数是;
(4)若该校九年级有500名学生,请你用此样本估计体育测试中A级和B级的学生人数约为多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com