
【题目】如图①,在△ABC中,∠BAC=90°,AB=AC,点E在AC上(且不与点A,C重合),在△ABC的外部作△CED,使∠CED=90°,DE=CE,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.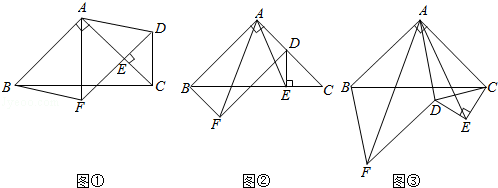
(1)请直接写出线段AF,AE的数量关系;
(2)将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
(3)在图②的基础上,将△CED绕点C继续逆时针旋转,请判断(2)问中的结论是否发生变化?若不变,结合图③写出证明过程;若变化,请说明理由.
【答案】
(1)AF= ![]() AE
AE
(2)
解:如图②中,结论:AF= ![]() AE.
AE.
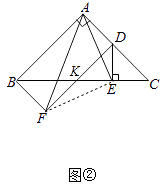
理由:连接EF,DF交BC于K.
∵四边形ABFD是平行四边形,
∴AB∥DF,
∴∠DKE=∠ABC=45°,
∴∠EKF=180°﹣∠DKE=135°,EK=ED,
∵∠ADE=180°﹣∠EDC=180°﹣45°=135°,
∴∠EKF=∠ADE,
∵∠DKC=∠C,
∴DK=DC,
∵DF=AB=AC,
∴KF=AD,
在△EKF和△EDA中,
 ,
,
∴△EKF≌△EDA,
∴EF=EA,∠KEF=∠AED,
∴∠FEA=∠BED=90°,
∴△AEF是等腰直角三角形,
∴AF= ![]() AE
AE
(3)
解:如图③中,结论不变,AF= ![]() AE.
AE.
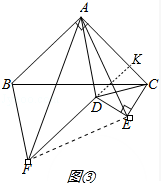
理由:连接EF,延长FD交AC于K.
∵∠EDF=180°﹣∠KDC﹣∠EDC=135°﹣∠KDC,
∠ACE=(90°﹣∠KDC)+∠DCE=135°﹣∠KDC,
∴∠EDF=∠ACE,
∵DF=AB,AB=AC,
∴DF=AC
在△EDF和△ECA中,
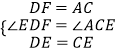 ,
,
∴△EDF≌△ECA,
∴EF=EA,∠FED=∠AEC,
∴∠FEA=∠DEC=90°,
∴△AEF是等腰直角三角形,
∴AF= ![]() AE
AE
【解析】解:(1)如图①中,结论:AF= ![]() AE.
AE.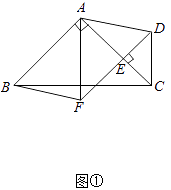
理由:∵四边形ABFD是平行四边形,
∴AB=DF,
∵AB=AC,
∴AC=DF,
∵DE=EC,
∴AE=EF,
∵∠DEC=∠AEF=90°,
∴△AEF是等腰直角三角形,
∴AF= ![]() AE.
AE.
故答案为AF= ![]() AE.
AE.
(1)如图①中,结论:AF= ![]() AE,只要证明△AEF是等腰直角三角形即可.(2)如图②中,结论:AF=
AE,只要证明△AEF是等腰直角三角形即可.(2)如图②中,结论:AF= ![]() AE,连接EF,DF交BC于K,先证明△EKF≌△EDA再证明△AEF是等腰直角三角形即可.(3)如图③中,结论不变,AF=
AE,连接EF,DF交BC于K,先证明△EKF≌△EDA再证明△AEF是等腰直角三角形即可.(3)如图③中,结论不变,AF= ![]() AE,连接EF,延长FD交AC于K,先证明△EDF≌△ECA,再证明△AEF是等腰直角三角形即可.
AE,连接EF,延长FD交AC于K,先证明△EDF≌△ECA,再证明△AEF是等腰直角三角形即可.


科目:初中数学 来源: 题型:
【题目】阅读材料:像![]() 、
、![]()
![]() 、
、![]() 两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式
两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式![]() 例如,
例如,![]() 与
与![]() 、
、![]() 与
与![]() 、
、![]() 与
与![]() 等都是互为有理化因式
等都是互为有理化因式![]() 在进行二次根式计算时,利用有理化因式,可以化去分母中的根号.
在进行二次根式计算时,利用有理化因式,可以化去分母中的根号.
例如;![]() ;
;![]() .
.
解答下列问题:
(1)![]() 与________互为有理化因式,将
与________互为有理化因式,将![]() 分母有理化得________;
分母有理化得________;
(2)计算:![]() ;
;
(3)己知有理数a、b满足![]() ,求a、b的值.
,求a、b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学完“有理数的运算”后,某中学七年级各班各选出5名学生组成一个代表队,在数学方老师的组织下进行一次知识竞赛,竞赛规则是:每队都分别给出50道题,答对一题得3分,不答或答错一题倒扣1分
(1)如果2班代表队最后得分142分,那么2班代表队回答对了多少道题?
(2)1班代表队的最后得分能为145分吗?请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 两边同除以
两边同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣![]() 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).
错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=AD,CB=CD,AB ∥ CD.
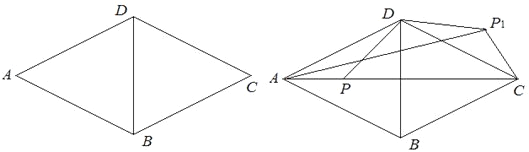
(1)求证:四边形ABCD是菱形.
(2)当△ABD满足什么条件时,四边形ABCD是正方形.(直接写出一个符合要求的条件).
(3)对角线AC和BD交于点O,∠ ADC =120°,AC=8, P为对角线AC上的一个动点,连接DP,将DP绕点D逆时针方向旋转120°得到线段DP1,直接写出A P1的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程(x﹣3)(x﹣2)﹣p2=0.
(1)求证:无论p取何值时,方程总有两个不相等的实数根;
(2)设方程两实数根分别为x1 , x2 , 且满足x12+x22=3x1x2 , 求实数p的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.
(1)如图1,若点O在BC上,求证:AB=AC;
(2)如图2,若点O在△ABC的内部,求证:AB=AC.
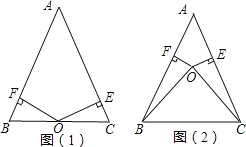
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形AOCD、正方形A1CC1D1、正方形A2C1C2D2的顶点A、A1、A2和O、C、C1、C2分别在一次函数y=x+1的图象和x轴上,若正比例函数y=kx则过点D5,则系数k的值是( )
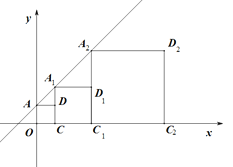
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com