
【题目】在学完“有理数的运算”后,某中学七年级各班各选出5名学生组成一个代表队,在数学方老师的组织下进行一次知识竞赛,竞赛规则是:每队都分别给出50道题,答对一题得3分,不答或答错一题倒扣1分
(1)如果2班代表队最后得分142分,那么2班代表队回答对了多少道题?
(2)1班代表队的最后得分能为145分吗?请简要说明理由.
 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】如图,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,连接CC′交斜边于点E,CC′的延长线交BB′于点F. 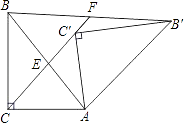
(1)证明:△ACE∽△FBE;
(2)设∠ABC=α,∠CAC′=β,试探索α、β满足什么关系时,△ACE与△FBE是全等三角形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲列车速度是60km/h,乙列车速度是90km/h.
(1)两列车都从某地出发,目的地距离出发点1000km,甲列车先走2小时,问乙列车什么时候能追上甲列车?追上时离目的地还有多远?
(2)甲列车从A地开往B地,乙列车同时从B地开往A地,已知A,B两地相距200km,两车相遇的地方离A地多远?(用方程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国务院办公厅2015年3月16日发布了《中国足球改革的总体方案》,这是中国足球历史上的重大改革.为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
获奖等次 | 频数 | 频率 |
一等奖 | 10 | 0.05 |
二等奖 | 20 | 0.10 |
三等奖 | 30 | b |
优胜奖 | a | 0.30 |
鼓励奖 | 80 | 0.40 |
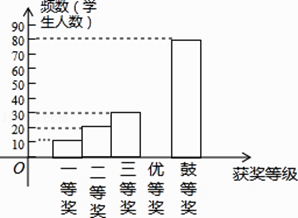
请根据所给信息,解答下列问题:
(1)a= , b= , 且补全频数分布直方图;
(2)若用扇形统计图来描述获奖分布情况,问获得优胜奖对应的扇形圆心角的度数是多少?
(3)在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表我市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是工人师傅用同一种材料制成的金属框架,已知![]() ,
,![]() ,
,![]() ,其中
,其中![]() 的周长为24cm,
的周长为24cm,![]() ,则制成整个金属框架所需这种材料的总长度为( )
,则制成整个金属框架所需这种材料的总长度为( )

A. 45cm B. 48cm C. 51cm D. 54cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司与销售人员签订了这样的工资合同:工资由两部分组成,一部分是基本工资,每人每月3000元;另一部分是按月销售量确定的奖励工资,每销售一件产品,奖励工资10元.设某销售员销售产品x件,他应得工资记为y元.
(1)求y与x的函数关系式.
(2)该销售员的工资为4100元,他这个月销售了多少件产品?
(3)要使每月工资超过4500元,该月的销售量应当超过多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,∠BAC=90°,AB=AC,点E在AC上(且不与点A,C重合),在△ABC的外部作△CED,使∠CED=90°,DE=CE,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.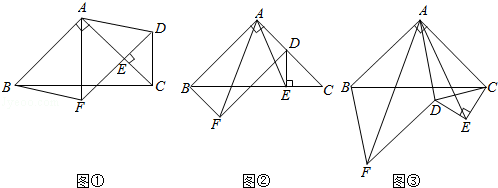
(1)请直接写出线段AF,AE的数量关系;
(2)将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
(3)在图②的基础上,将△CED绕点C继续逆时针旋转,请判断(2)问中的结论是否发生变化?若不变,结合图③写出证明过程;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国宋朝数学家杨辉在他的著作![]() 详解九章算法
详解九章算法![]() 中提出“杨辉三角”
中提出“杨辉三角”![]() 如图
如图![]() ,此图揭示了
,此图揭示了![]() 为非负整数
为非负整数![]() 展开式的项数及各项系数的有关规律.
展开式的项数及各项系数的有关规律.
例如:![]() ,它只有一项,系数为1;系数和为1;
,它只有一项,系数为1;系数和为1;
![]() ,它有两项,系数分别为1,1,系数和为2;
,它有两项,系数分别为1,1,系数和为2;
![]() ,它有三项,系数分别为1,2,1,系数和为4;
,它有三项,系数分别为1,2,1,系数和为4;
![]() ,它有四项,系数分别为1,3,3,1,系数和为8;
,它有四项,系数分别为1,3,3,1,系数和为8;![]() ,
,
则![]() 的展开式共有______项,系数和为______.
的展开式共有______项,系数和为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com