
【题目】如图,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,连接CC′交斜边于点E,CC′的延长线交BB′于点F. 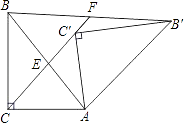
(1)证明:△ACE∽△FBE;
(2)设∠ABC=α,∠CAC′=β,试探索α、β满足什么关系时,△ACE与△FBE是全等三角形,并说明理由.
【答案】
(1)证明:∵Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,
∴AC=AC′,AB=AB′,∠CAB=∠C′AB′,
∴∠CAB+∠BAC′=∠C′AB′+∠BAC′,即∠CAC′=∠BAB′,
∴∠ABB′=∠AB′B=∠ACC′=∠AC′C,
∴∠ACC′=∠ABB′,
又∵∠AEC=∠FEB,
∴△ACE∽△FBE
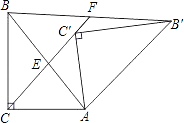
(2)解:当β=2α时,△ACE≌△FBE.
在△ACC′中,
∵AC=AC′,
∴∠ACC′= ![]() =
= ![]() =90°﹣α,
=90°﹣α,
在Rt△ABC中,
∠ACC′+∠BCE=90°,即90°﹣α+∠BCE=90°,
∴∠BCE=α,
∵∠ABC=α,
∴∠ABC=∠BCE,
∴CE=BE,
由(1)知:△ACE∽△FBE,
∴∠BEF=∠CEA,∠FBE=∠ACE,
又∵CE=BE,
∴△ACE≌△FBE
【解析】(1)欲证△ACE∽△FBE,通过观察发现两个三角形已经具备一组角对应相等,即∠AEC=∠FEB,此时,再证∠AC′C=∠ABB′即可.(2)欲证△ACE≌△FBE,由(1)知△ACE∽△FBE,只需证明CE=BE,由已知可证∠ABC=∠BCE=α,即证β=2α时,△ACE≌△FBE.
【考点精析】解答此题的关键在于理解相似三角形的判定的相关知识,掌握相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS),以及对旋转的性质的理解,了解①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.


科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,CE⊥AB交AB延长线于点E,点F为点B关于CE的对称点,连接CF,分别延长DC,CF至点G,H,使FH=CG,连接AG,DH交于点P.
(1)依题意补全图1;
(2)猜想AG和DH的数量关系并证明;
(3)若∠DAB=70°,是否存在点G,使得△ADP为等边三角形?若存在,求出CG的长;若不存在,说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE= ![]() AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )
AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( ) 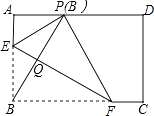
A.①②
B.②③
C.①③
D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,第35秒时,点E在量角器上对应的读数是度. 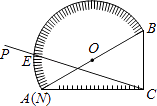
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(﹣3,2),(b,m),(c,m),则点E的坐标是( ) 
A.(2,﹣3)
B.(2,3)
C.(3,2)
D.(3,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.

(1)求证:△ABE≌△CDF;
(2)若AC与BD交于点O,求证:AO=CO.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:像![]() 、
、![]()
![]() 、
、![]() 两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式
两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式![]() 例如,
例如,![]() 与
与![]() 、
、![]() 与
与![]() 、
、![]() 与
与![]() 等都是互为有理化因式
等都是互为有理化因式![]() 在进行二次根式计算时,利用有理化因式,可以化去分母中的根号.
在进行二次根式计算时,利用有理化因式,可以化去分母中的根号.
例如;![]() ;
;![]() .
.
解答下列问题:
(1)![]() 与________互为有理化因式,将
与________互为有理化因式,将![]() 分母有理化得________;
分母有理化得________;
(2)计算:![]() ;
;
(3)己知有理数a、b满足![]() ,求a、b的值.
,求a、b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学完“有理数的运算”后,某中学七年级各班各选出5名学生组成一个代表队,在数学方老师的组织下进行一次知识竞赛,竞赛规则是:每队都分别给出50道题,答对一题得3分,不答或答错一题倒扣1分
(1)如果2班代表队最后得分142分,那么2班代表队回答对了多少道题?
(2)1班代表队的最后得分能为145分吗?请简要说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com