
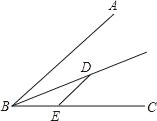
【题目】如图,∠ABC=50°,BD平分∠ABC,过D作DE∥AB交BC于点E,若点F在AB上,且满足DF=DE,则∠DFB的度数为_____.
【答案】50°或130°.
【解析】
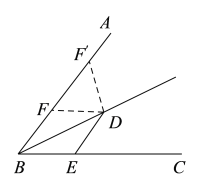
由题意可知,点F的位置存在如下图所示的两种情况(在点F处或点F′处),根据图形结合“已知条件”利用“角的两边关于角平分线对称和等腰三角形的性质”进行分析解答即可.
如下图,∵DE∥AB,
∴∠DEC=∠ABC=50°,
∴∠DEB=180°-50°=130°,
(1)当点F在AB边上的F处时,由DF=DE和BD平方∠ABC可知,
此时△BDF和△BDE关于BD对称,
∴△BDF≌△BDE,
∴∠DFB=∠DEB=130°;
(2)当点F在AB边上的F′处时,
∵DF′=DE=DF,
∴∠DF′B=∠DFF′,
又∵∠DFF′=180°-∠DFB=50°,
∴∠DF′B=50°;
综上所述,∠DFB=50°或130°.
故答案为:50°或130°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
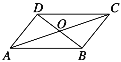
【题目】四边形![]() 中,对角线
中,对角线![]() 、
、![]() 相交于点
相交于点![]() ,下列条件不能判定这个四边形是平行四边形的是( )
,下列条件不能判定这个四边形是平行四边形的是( )
A. AB∥DC,AD∥BC B. AO=CO,BO=DO
C. AB∥DC,AD=BC D. AB=DC,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点E,F分别是ABCD的边BC,AD上的中点,且∠BAC=90°. 
(1)求证:四边形AECF是菱形;
(2)若∠B=30°,BC=10,求菱形AECF面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,∠BAC=90°,AB=AC,点E在AC上(且不与点A,C重合),在△ABC的外部作△CED,使∠CED=90°,DE=CE,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.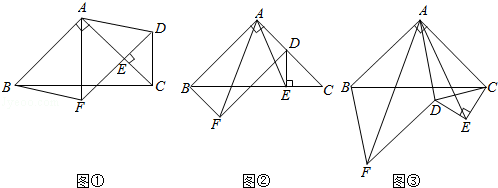
(1)请直接写出线段AF,AE的数量关系;
(2)将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
(3)在图②的基础上,将△CED绕点C继续逆时针旋转,请判断(2)问中的结论是否发生变化?若不变,结合图③写出证明过程;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ADB、△BCD都是等边三角形,点E,F分别是AB,AD上两个动点,满足AE=DF.连接BF与DE相交于点G,CH⊥BF,垂足为H,连接CG.若DG=![]() ,BG=
,BG=![]() ,且
,且![]() 、
、![]() 满足下列关系:
满足下列关系:![]() ,
,![]() ,则GH= .
,则GH= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,
组别 | 课堂发言次数n |
A | 0≤n<3 |
B | 3≤n<6 |
C | 6≤n<9 |
D | 9≤n<12 |
E | 12≤n<15 |
F | 15≤n<18 |
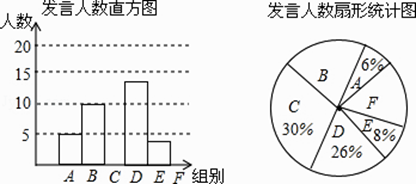
请结合图中相关数据回答下列问题:
(1)样本容量是 , 并补全直方图;
(2)该年级共有学生800人,请估计该年级在这天里发言次数不少于12次的人数;
(3)已知A组发言的学生中恰好有1位女生,E组发言的学生中有2位男生,现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好都是男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工艺品厂计划一周生产工艺品2100个,平均每天生产300个,但实际每天生产量与计划相比有出入.下表是某周的生产情况 (超产记为正,减产记为负):

(1) 写出该厂星期一生产工艺品的数量.
(2) 本周产量最多的一天比最少的一天多生产多少个工艺品?
(3) 请求出该工艺品厂在本周实际生产工艺品的数量.
(4) 已知该厂实行每周计件工资制,每生产一个工艺品可得60元,若超额完成任务,则超过部分每个可得50元,少生产一个扣80元.试求该工艺厂在这一周应付出的工资总额.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com