
����Ŀ��ͬѧ�Ƕ�֪����|5������2��|��ʾ5�멁2֮��ľ���ֵ��ʵ����Ҳ������Ϊ5�멁2����������������Ӧ������֮��ľ��룮������������������̽����
![]()
��1�������ϱ�ʾ5�멁2����֮��ľ������� ��
��2�������ϱ�ʾx��2������֮��ľ�����Ա�ʾΪ�� ����
��3��ͬ��|x+3|+|x��1|��ʾ������������x����Ӧ�ĵ㵽��3��1����Ӧ�ĵ�ľ���֮�ͣ������ҳ����з�������������x��ʹ��|x+3|+|x��1|=4���������������� ����
��4��������̽������|x+10|+|x+2|+|x��8|�Ƿ�����Сֵ������У�ֱ��д����Сֵ�����û�У�˵�����ɣ�
��5��������̽������|x+10|+|x+2|+|x��8|+|x��10|�Ƿ�����Сֵ������У�ֱ��д����Сֵ�����û�У�˵�����ɣ�
���𰸡���1��7����2��|x��2|����3����2����1��0��1����4��18����5��20.
��������
��1�����ݾ��빫ʽ���ɽ��
��2�����ݾ��빫ʽ���ɽ����
��3�����þ���ֵ��������⼴�ɣ�
��4�����þ���ֵ��������⼴�ɣ�
��5���������ἰ����ֵ�����ɽ��
��1�������ϱ�ʾ5�멁2����֮��ľ����ǣ�5������2��=7��
�ʴ�Ϊ7��
��2�������ϱ�ʾx��2������֮��ľ�����Ա�ʾΪ|x��2|��
�ʴ�Ϊ��|x��2|��
��3����|x+3|+|x��1|��ʾ������������x����Ӧ�ĵ㵽��3��1����Ӧ�ĵ�ľ���֮�ͣ�|x+3|+|x��1|=4��
��������������2����1��0��1��
�ʴ�Ϊ����2����1��0��1��
��4������Сֵ��
�����ǣ���|x+10|+|x+2|+|x��8|����Ϊ���������ϱ�ʾx����10����2��8�ľ���֮�ͣ�
�൱x�ک�10��8֮����߶��ϣ�����10��x��8��ʱ��
��|x+10|+|x+2|+|x��8|��ֵ����Сֵ����СֵΪ10+8=18��
��5������Сֵ��
������|x+10|+|x+2|+|x��8|+|x��10|����Ϊ���������ϱ�ʾx����10����2��8��10�ľ���֮�ͣ�
�൱x�ک�10��10֮����߶��ϣ�����10��x��10��ʱ��
��|x+10|+|x+2|+|x��8|+|x��10|��ֵ����Сֵ����СֵΪ10+10=20��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��y=--![]() x��8��x�ᣬy��ֱ��ڵ�A����B����D��y��ĸ������ϣ�������DAB��ֱ��AD�۵�����Bǡ������x���������ϵĵ�C����
x��8��x�ᣬy��ֱ��ڵ�A����B����D��y��ĸ������ϣ�������DAB��ֱ��AD�۵�����Bǡ������x���������ϵĵ�C����
(1)��AB�ij��͵�C�����ꣻ
(2)��ֱ��CD�ı���ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ֱ����ֱ�����ǰ�ABC��б��AB�غϣ�����������0�̶��ߵĶ˵�N���A�غϣ�����CP��CA��������˳ʱ�뷽����ÿ��2�ȵ��ٶ���ת��CP���������İ�Բ�����ڵ�E����35��ʱ����E���������϶�Ӧ�Ķ������ȣ� 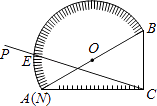
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AB=CD��BF=DE��AE��BD��CF��BD������ֱ�ΪE��F��

��1����֤����ABE�ա�CDF��
��2����AC��BD���ڵ�O����֤��AO=CO��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڴ�¥AB����ǰ����һб��CD��CD=4�ף��½ǡ�DCE=30�㣬С����б���µĵ�C�����¥��B������Ϊ60�㣬��б���ϵĵ�D�����¥��B������Ϊ45�㣬���е�A��C��E��ͬһֱ���ϣ�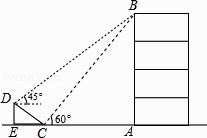
��1����б��CD�ĸ߶�DE��
��2�����¥AB�ĸ߶ȣ�����������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ���![]() ��
��![]()
![]() ��
��![]() �������ж��θ�ʽ�Ĵ���ʽ��ˣ��������ж��θ�ʽ�����dz�����������ʽ��Ϊ��������ʽ
�������ж��θ�ʽ�Ĵ���ʽ��ˣ��������ж��θ�ʽ�����dz�����������ʽ��Ϊ��������ʽ![]() ���磬
���磬![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ȶ��ǻ�Ϊ��������ʽ
�ȶ��ǻ�Ϊ��������ʽ![]() �ڽ��ж��θ�ʽ����ʱ��������������ʽ�����Ի�ȥ��ĸ�еĸ��ţ�
�ڽ��ж��θ�ʽ����ʱ��������������ʽ�����Ի�ȥ��ĸ�еĸ��ţ�
���磻![]() ��
��![]() ��
��
����������⣺
��1��![]() ��________��Ϊ��������ʽ����
��________��Ϊ��������ʽ����![]() ��ĸ��������________��
��ĸ��������________��
��2�����㣺![]() ��
��
��3����֪������a��b����![]() ����a��b��ֵ��
����a��b��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ� ��
A.��һö�ʵؾ��ȵ����������ӣ�����ֹͣת����5�㳯���DZ�Ȼ�¼�
B.������������Щѧ���Դ����ʺ��ó������鷨
C.������������ͬ�����¸����10�Σ����ǵijɼ���ƽ������ͬ������ֱ���S��2=0.4��S��2=0.6���������ɼ����ȶ�
D.����ö�ʵؾ��ȵ�Ӳ�ң�����öӲ�Ҷ������泯�ϡ���һ�¼������ĸ���Ϊ ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����У�һ�����ӿ�����6�ˣ�����Ѷ������Ӱ���һ�𣬿������������ְڷŷ�ʽ��
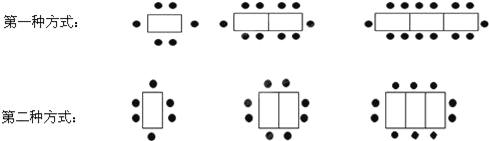
��1������5������ʱ����һ�ְڷŷ�ʽ���������ˣ��ڶ��ְڷŷ�ʽ���������ˣ�
��2������n������ʱ����һ�ְڷŷ�ʽ���������ˣ��ڶ��ְڷŷ�ʽ���������ˣ�
��3��һ���������Ҫ�Ӵ�98λ�˿�ͬ�Ͳͣ�������Ҫ����һ�𣩣�������ֻ��25�������IJ�������������������ľ����������ѡ�����ַ�ʽ���ڷŲ�����Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У�AB=AD��CB=CD��AB �� CD.
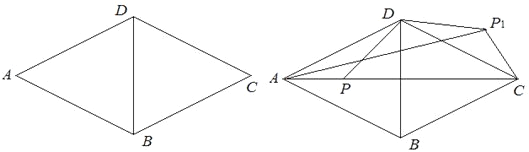
��1����֤���ı���ABCD������.
��2������ABD����ʲô����ʱ���ı���ABCD��������.��ֱ��д��һ������Ҫ���������.
��3���Խ���AC��BD���ڵ�O���� ADC =120�㣬AC=8�� PΪ�Խ���AC�ϵ�һ�����㣬����DP����DP�Ƶ�D��ʱ�뷽����ת120��õ��߶�DP1��ֱ��д��A P1��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com