
 如图,Rt△ABC中,∠ACB=90°,∠B=30°,AB=12cm,以AC为直径的半圆O交AB于点D,点E是AB的中点,CE交半圆O于点F,则图中阴影部分的面积为________cm2.
如图,Rt△ABC中,∠ACB=90°,∠B=30°,AB=12cm,以AC为直径的半圆O交AB于点D,点E是AB的中点,CE交半圆O于点F,则图中阴影部分的面积为________cm2. )
) 与弦AD围成的弓形的面积等于
与弦AD围成的弓形的面积等于 与弦CF围成的弓形的面积相等,则阴影部分的面积等于半圆的面积减去直角△ACD的面积,再减去弓形的面积,据此即可求解.
与弦CF围成的弓形的面积相等,则阴影部分的面积等于半圆的面积减去直角△ACD的面积,再减去弓形的面积,据此即可求解.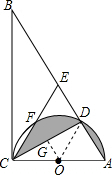 解:∵Rt△ABC中,∠ACB=90°,∠B=30°,AB=12cm,
解:∵Rt△ABC中,∠ACB=90°,∠B=30°,AB=12cm, AB=6cm,∠A=60°
AB=6cm,∠A=60° AB,
AB,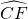 =
= ,
, OC=
OC= ,CG=
,CG= CD=
CD= .
. -
- ×
× ×
× =3π-
=3π- .
. .
. 与弦AD围成的弓形的面积等于
与弦AD围成的弓形的面积等于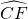 与弦CF围成的弓形的面积相等是关键.
与弦CF围成的弓形的面积相等是关键. 

 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,Rt△ABC中,∠ACB=90°,tanB=
如图,Rt△ABC中,∠ACB=90°,tanB=| 3 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F.
如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com