

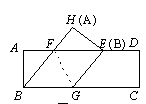

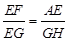 ,∴EF=5,
,∴EF=5,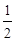 EF·EG=
EF·EG=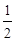 ×5×10=25.
×5×10=25.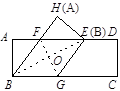
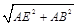 =8
=8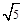 ,∴BO=4
,∴BO=4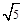 ,
,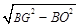 =4
=4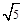 。
。

科目:初中数学 来源:不详 题型:解答题
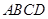 中,
中,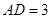 厘米,
厘米,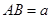 厘米(
厘米(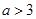 ).动点
).动点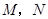 同时从
同时从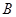 点出发,分别沿
点出发,分别沿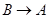 ,
,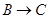 运动,速度是
运动,速度是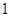 厘米/秒.过
厘米/秒.过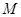 作直线垂直于
作直线垂直于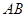 ,分别交
,分别交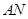 ,
,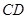 于
于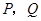 .当点
.当点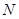 到达终点
到达终点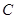 时,点
时,点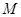 也随之停止运动.设运动时间为
也随之停止运动.设运动时间为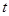 秒.
秒.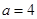 厘米,
厘米,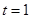 秒,则
秒,则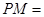 ______厘米;
______厘米;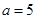 厘米,求时间
厘米,求时间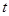 ,使
,使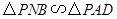 ,并求出它们的相似比;
,并求出它们的相似比;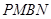 与梯形
与梯形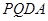 的面积相等,求
的面积相等,求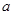 的取值范围;
的取值范围;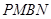 ,梯形
,梯形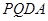 ,梯形
,梯形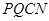 的面积都相等?若存在,求
的面积都相等?若存在,求 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.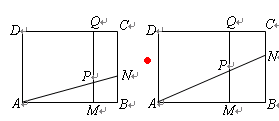
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
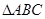 中,
中, ,
, ,
,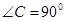 .
.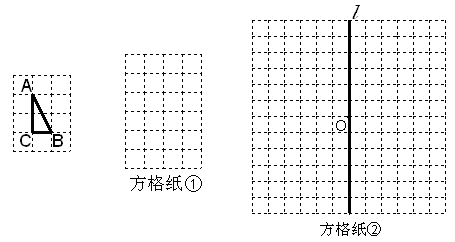
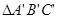 ,使
,使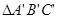 ∽
∽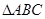 ,且相似比为2︰1;
,且相似比为2︰1;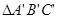 称为“基本图形”,请你利用“基本图形”,借助旋转、平移或轴对称变换,在方格纸②中设计一个以点
称为“基本图形”,请你利用“基本图形”,借助旋转、平移或轴对称变换,在方格纸②中设计一个以点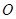 为对称中心,并且以直线
为对称中心,并且以直线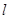 为对称轴的图案.
为对称轴的图案.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com