
【题目】如图,抛物线y=﹣x2+2x+3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C. 
(1)将抛物线沿y轴平移t(t>0)个单位,当平移后的抛物线与线段OB有且只有一个交点时,则t的取值范围是 .
(2)抛物线上存在点P,使∠BCP=∠BAC﹣∠ACO,则点P的坐标为 .
【答案】
(1)0<t<3或t=4
(2)( ![]() ,
, ![]() )或(﹣5,﹣32)
)或(﹣5,﹣32)
【解析】解:(1)由题意,抛物线只能沿y轴向下平移, ∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴设平移后的抛物线的解析式为y=﹣(x﹣1)2+4﹣t(t>0),
当原点O落在平移后的抛物线上时,把(0,0)代入得:
0=﹣(0﹣1)2+4﹣t,
解得t=3;
当平移后的抛物线的顶点落在x轴上时,x=1,y=0
即0=﹣(1﹣1)2+4﹣t,
解得t=4,
∵平移后的抛物线与线段OB有且只有一个交点
∴0<t<3或t=4,
故答案为:0<t<3或t=4;
⑵当y=0时,﹣x2+2x+3=0,
解得:x=﹣1或x=3,
即A(﹣1,0)、B(3,0),
取AC的中点M,过M作MN⊥AC交OC于N,连接AN,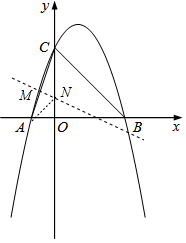
则AN=CN,
∴∠ACO=∠CAN
∵∠BCP=∠BAC﹣∠ACO,
∴∠BCP=∠BAC﹣∠CAN=∠NAO
∵∠ACO=∠NCM,∠AOC=∠CMN=90°,
∴△MCN∽△OCA,
∴ ![]() =
= ![]() ,
,
∴CN= ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∴NO=CO﹣CN=3﹣ ![]() =
= ![]() ,
,
∴tan∠NAO= ![]() =
= ![]() ;
;
当点P在BC上方时,设为P1 , 过B作BD⊥BC交直线CP1于D,过D作DE⊥x轴于E
∵∠OCB=∠DBE,∠BOC=∠BED=90°,
∴△BDE∽△CBO,
∴ ![]() =
= ![]() =
= ![]() =tan∠BCP1=tan∠NAO=
=tan∠BCP1=tan∠NAO= ![]() ,
,
∴BE= ![]() CO=4,DE=
CO=4,DE= ![]() BO=4,OE=3+4=7
BO=4,OE=3+4=7
∴D(7,4)
设直线CP1的解析式为y=k1x+3,把(7,4)代入
4=7k1+3,
∴k1= ![]() ,
,
∴y= ![]() x+3
x+3
令﹣x2+2x+3= ![]() x+3,
x+3,
解得x1=0(舍去),x2= ![]()
∴P1( ![]() ,
, ![]() ),
),
当点P在BC下方时,设为P2(m,n),
则∠BCP2=∠BCP1
延长DB交直线CP2于E,则点B是DE的中点
∴ 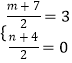
解得 ![]() ,
,
∴E(﹣1,﹣4)
设直线CP2的解析式为y=k2x+3,把(﹣1,﹣4)代入﹣4=﹣k2+3,
∴k2=7,
∴y=7x+3
令﹣x2+2x+3=7x+3,
解得x1=0(舍去),x2=﹣5
∴P2(﹣5,﹣32)
综上所述,抛物线上存在点P,使∠BCP=∠BAC﹣∠ACO,
P点坐标为( ![]() ,
, ![]() )或(﹣5,﹣32),
)或(﹣5,﹣32),
故答案为:( ![]() ,
, ![]() )或(﹣5,﹣32).
)或(﹣5,﹣32).
(1)把函数化为顶点式y=a(x﹣h)2+k的形式,向下平移使抛物线与x轴只有一个交点,即把解析式中的k变成0即可.(2)取AC的中点M,过M作MN⊥AC交OC于N,连接AN则AN=CN,∠ACO=∠CAN,通过△MCN∽△OCA,求得CN的值,进而求得NO的值,从而得出tan∠NAO= ![]() =
= ![]() ;当P在BC的上方时,设为P1 , 过B作BD⊥BC交直线CP1于D,过D作DE⊥x轴于E,通过证明△BDE∽△CBO,进而求得tan∠BCP1=tan∠NAO=
;当P在BC的上方时,设为P1 , 过B作BD⊥BC交直线CP1于D,过D作DE⊥x轴于E,通过证明△BDE∽△CBO,进而求得tan∠BCP1=tan∠NAO= ![]() ,从而确定D点的坐标,把D点代入直线CP1的解析式为y=k1x+3,求得P1点的坐标;当点P在BC下方时,设为P2(m,n),则∠BCP2=∠BCP1 , 延长DB交直线CP2于E,则点B是DE的中点,求得E点坐标,代入直线CP2的解析式为y=k2x+3,即可求得P2的坐标.
,从而确定D点的坐标,把D点代入直线CP1的解析式为y=k1x+3,求得P1点的坐标;当点P在BC下方时,设为P2(m,n),则∠BCP2=∠BCP1 , 延长DB交直线CP2于E,则点B是DE的中点,求得E点坐标,代入直线CP2的解析式为y=k2x+3,即可求得P2的坐标.


科目:初中数学 来源: 题型:
【题目】某中学开展“阳光体育一小时”活动,根据学校实际情况,如图决定开设“A:踢毽子,B:篮球,C:跳绳,D:乒乓球”四项运动项目(每位同学必须选择一项),为了解学生最喜欢哪一项运动项目,随机抽取了一部分学生进行调查,丙将调查结果绘制成如图的统计图,则参加调查的学生中最喜欢跳绳运动项目的学生数为( )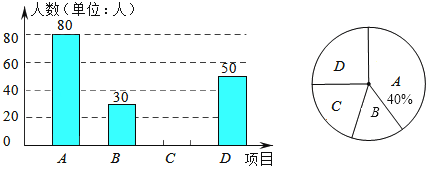
A.240
B.120
C.80
D.40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x2﹣4x+3与x轴交于A、B两点(点A在点B的左侧),点C是此抛物线的顶点.
(1)求点A、B、C的坐标;
(2)点C在反比例函数![]() (k≠0)的图象上,求反比例函数的解析式.
(k≠0)的图象上,求反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在﹣3、﹣2、﹣1、0、1、2这六个数中,随机取出一个数,记为m,若数m使关于x的分式方程 ![]() ﹣1=
﹣1= ![]() 的解是正实数或零,且使得的二次函数y=﹣x2+(2m﹣1)x+1的图象,在x>1时,y随x的增大而减小,则满足条件的所有m之和是( )
的解是正实数或零,且使得的二次函数y=﹣x2+(2m﹣1)x+1的图象,在x>1时,y随x的增大而减小,则满足条件的所有m之和是( )
A.﹣2
B.﹣1
C.0
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个四位数,记千位上和百位上的数字之和为x,十位上和个位上的数字之和为y,如果x=y,那么称这个四位数为“和平数”. 例如:1423,x=1+4,y=2+3,因为x=y,所以1423是“和平数”.
(1)直接写出:最小的“和平数”是 , 最大的“和平数”是;
(2)求个位上的数字是千位上的数字的两倍且百位上的数字与十位上的数字之和是12的倍数的所有“和平数”;
(3)将一个“和平数”的个位上与十位上的数字交换位置,同时,将百位上与千位上的数字交换位置,称交换前后的这两个“和平数”为一组“相关和平数”. 例如:1423与4132为一组“相关和平数”
求证:任意的一组“相关和平数”之和是1111的倍数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店尝试用单价随天数而变化的销售模式销售一种商品,利用30天的时间销售一种成本为10元/件的商品售后,经过统计得到此商品单价在第x天(x为正整数)销售的相关信息,如表所示:
销售量n(件) | n=50﹣x |
销售单价m(元/件) | 当1≤x≤20时,m=20+ |
当21≤x≤30时,m=10+ |
(1)请计算第几天该商品单价为25元/件?
(2)求网店销售该商品30天里所获利润y(元)关于x(天)的函数关系式;
(3)这30天中第几天获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张正面分别标有数字﹣1,0,1,2的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上洗均匀.
(1)随机抽取一张卡片,求抽到数字“﹣1”的概率;
(2)随机抽取一张卡片,然后不放回,再随机抽取一张卡片,请用列表或画树状图的方法求出第一次抽到数字“2”且第二次抽到数字“0”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+b2 , 其中正确结论是(填序号)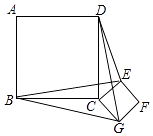
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com